��Ŀ����
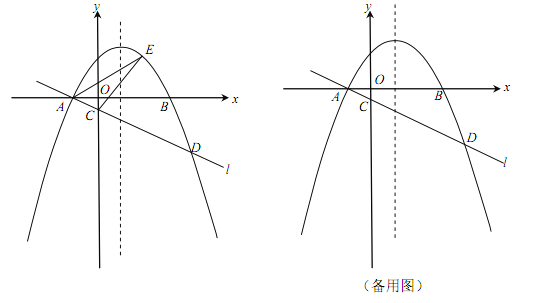
����Ŀ������С������12�֣���ͼ����ƽ��ֱ������ϵxOy�У�������![]() ��
��![]() ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��������A��ֱ��l��
����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��������A��ֱ��l��![]() ��y�Ḻ���ύ�ڵ�C���������ߵ���һ������ΪD����CD=4AC��
��y�Ḻ���ύ�ڵ�C���������ߵ���һ������ΪD����CD=4AC��
��1��ֱ��д����A�����꣬����ֱ��l�ĺ�������ʽ������k��b�ú�a��ʽ�ӱ�ʾ����
��2����E��ֱ��l�Ϸ����������ϵĶ��㣬����ACE����������ֵΪ![]() ����a��ֵ��
����a��ֵ��
��3����P�������ߵĶԳ����ϵ�һ�㣬��Q���������ϣ��Ե�A��D��P��QΪ������ı����ܷ��Ϊ���Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��A����1��0����![]() ����2��
����2��![]() ����3��P��������1��
����3��P��������1��![]() ����1����4����
����1����4����
��������
���⣨1����![]() �У���y=0���õ�
�У���y=0���õ�![]() ��
��![]() ���õ�A����1��0����B��3��0������ֱ��l������A���õ�
���õ�A����1��0����B��3��0������ֱ��l������A���õ�![]() ����
����![]() ����
����![]() ����
����![]() ������CD��4AC���ʵ�D�ĺ�����Ϊ4������
������CD��4AC���ʵ�D�ĺ�����Ϊ4������![]() ���õ�
���õ�![]() ���Ӷ��ó�ֱ��l�ĺ�������ʽ��
���Ӷ��ó�ֱ��l�ĺ�������ʽ��
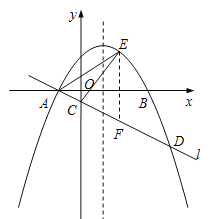
��2������E��EF��y�ᣬ��ֱ��l�ڵ�F����E��![]() ��
��![]() ������F��
������F��![]() ��
��![]() ����
����
EF��![]() =
=![]() ��S��ACE��S��AFE��S��CFE��
��S��ACE��S��AFE��S��CFE��![]() ��
��![]() ������ACE����������ֵΪ
������ACE����������ֵΪ![]() ������ACE����������ֵΪ
������ACE����������ֵΪ![]() ������
������![]() �����
�����![]() ��
��
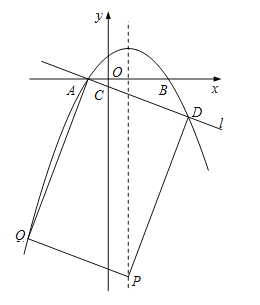
��3����![]() ����
����![]() �����
�����![]() ��
��![]() ���õ�D��4��5a������Ϊ�����ߵĶԳ���Ϊ
���õ�D��4��5a������Ϊ�����ߵĶԳ���Ϊ![]() ����P��1��m����Ȼ�������������ۣ�����AD�Ǿ��ε�һ���ߣ�����AD�Ǿ��ε�һ���Խ��ߣ�
����P��1��m����Ȼ�������������ۣ�����AD�Ǿ��ε�һ���ߣ�����AD�Ǿ��ε�һ���Խ��ߣ�
�����������1����![]() =
=![]() ����y=0���õ�
����y=0���õ�![]() ��
��![]() ����A����1��0����B��3��0������ֱ��l������A����
����A����1��0����B��3��0������ֱ��l������A����![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() ����CD��4AC������D�ĺ�����Ϊ4����
����CD��4AC������D�ĺ�����Ϊ4����![]() ����
����![]() ����ֱ��l�ĺ�������ʽΪ
����ֱ��l�ĺ�������ʽΪ![]() ��
��
��2������E��EF��y�ᣬ��ֱ��l�ڵ�F����E��![]() ��
��![]() ������F��
������F��![]() ��
��![]() ����
����
EF��![]() =
=![]() ��
��
S��ACE��S��AFE��S��CFE��![]()
��![]() ��
��![]() ��
��
���ACE����������ֵΪ![]() ���ߡ�ACE����������ֵΪ
���ߡ�ACE����������ֵΪ![]() ����
����![]() �����
�����![]() ��
��
��3����![]() ����
����![]() �����
�����![]() ��
��![]() ����D��4��5a������
����D��4��5a������![]() ���������ߵĶԳ���Ϊ
���������ߵĶԳ���Ϊ![]() ����P��1��m����
����P��1��m����
����AD�Ǿ��ε�һ���ߣ���Q����4��21a����m��21a��5a��26a����P��1��26a�������ı���ADPQΪ���Σ����ADP��90������![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ����P1��1��
����P1��1��![]() ����
����
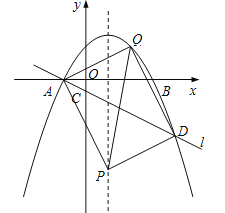
����AD�Ǿ��ε�һ���Խ��ߣ����߶�AD���е�����Ϊ��![]() ��
��![]() ����Q��2��
����Q��2��![]() ����m��
����m��![]() ����P��1��8a�������ı���APDQΪ���Σ����APD��90������
����P��1��8a�������ı���APDQΪ���Σ����APD��90������![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ����P2��1����4����
����P2��1����4����
�����������Ե�A��D��P��QΪ������ı����ܳ�Ϊ���Σ���P������Ϊ��1��![]() ����1����4����
����1����4����

����Ŀ��ij��˾��2014�꿪ʼͶ�뼼���Ľ��ʽ𣬾������Ľ������Ʒ�ijɱ����Ͻ��ͣ������������±���
�� �� | 2013 | 2014 | 2015 | 2016 |
Ͷ�뼼���ʽ� | 2.5 | 3 | 4 | 4.5 |
��Ʒ�ɱ� | 7.2 | 6 | 4.5 | 4 |
��1��������������������ݣ���һ�κ����ͷ�����������ȷ����һ�������ܱ�ʾ��仯���ɣ��������ɣ�����������ʽ��
��2���������ֱ仯���ɣ���2017����Ͷ���ʽ�5��Ԫ.
��Ԥ�������ɱ�ÿ����2016�꽵�Ͷ�����Ԫ��
����������2017���ÿ����Ʒ�ɱ����͵�3.2��Ԫ������ҪͶ�뼼���ʽ������Ԫ���������ȷ��0.01��Ԫ��.
����Ŀ���Ķ�С��������ķ����������2![]() ��3x��0��
��3x��0��
�ⷨ1���� ԭ���̻�Ϊ2t��3t2��0 �ⷽ��2t��3t2��0����t1��0��t2�� ���� ������ ��x��0�� �����飬x��0�� ���ԣ�ԭ���̵Ľ���x��0�� | �ⷨ2�������2 ��������ͬʱƽ������4x��9x2�� �ⷽ��4x��9x2����x��0�� �����飬x��0�� ���ԣ�ԭ���̵Ľ���x��0�� |
���������ijһ�ַ������������x��![]() ����1�Ľ⣮
����1�Ľ⣮