题目内容
图(1)是棱长为1的小正方体,图(2)、图(3)是由这样的正方体摆放而成,按照这样的方法 继续摆放,自上而下分别叫第1层、第2层…第n层,第n层小正方体个数记为S,如表.
继续摆放,自上而下分别叫第1层、第2层…第n层,第n层小正方体个数记为S,如表.| l | 1 | 2 | 3 | 4 | … |
| S | 1 | 3 | 6 | 10 | … |
分析:由图形可知,其第一层有1个,第二层有(1+2)个,第三层有(1+2+3)个,从而推出第n层的规律,然后把n=100代入,即可求出对应的S的值.
解答:解:∵第一层:1个;
第二层:3个,3=1+2;
第三层:6个,6=1+2+3;
第四层:10个,10=1+2+3+4;
…
∴第n层:1+2+3+…+n=
n(n+1)个.
∴当n=100 时,S=
×100×101=5050.
故答案为:5050.
第二层:3个,3=1+2;
第三层:6个,6=1+2+3;
第四层:10个,10=1+2+3+4;
…
∴第n层:1+2+3+…+n=
| 1 |
| 2 |
∴当n=100 时,S=
| 1 |
| 2 |
故答案为:5050.
点评:本题主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后直接利用规律求解.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
图(1)是棱长为1的小正方体,图(2)、图(3)是由这样的正方体摆放而成,按照这样的方法 继续摆放,自上而下分别叫第1层、第2层…第n层,第n层小正方体个数记为S,如表.
继续摆放,自上而下分别叫第1层、第2层…第n层,第n层小正方体个数记为S,如表.
| l | 1 | 2 | 3 | 4 | … |
| S | 1 | 3 | 6 | 10 | … |
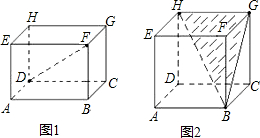 观察图(1),阅读理解关于长方体的对角线长定理:长方体一条对角线长的平方等于一个顶点上三条棱的长的平方和.用符号表示即:DF2=FE2+FB2+FG2.应用这个定理尝试解决下列问题:已知图(2)是棱长为3cm的立方体,那么该立方体的对角线HB为
观察图(1),阅读理解关于长方体的对角线长定理:长方体一条对角线长的平方等于一个顶点上三条棱的长的平方和.用符号表示即:DF2=FE2+FB2+FG2.应用这个定理尝试解决下列问题:已知图(2)是棱长为3cm的立方体,那么该立方体的对角线HB为
