题目内容

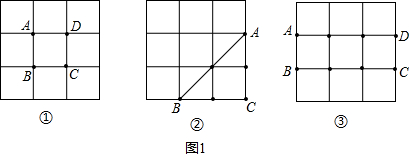
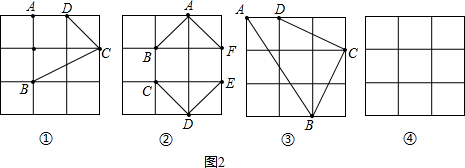
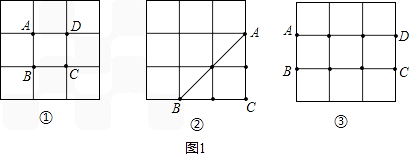
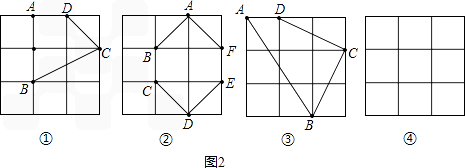
观察图（1），阅读理解关于长方体的对角线长定理：长方体一条对角线长的平方等于一个顶点上三条棱的长的平方和．用符号表示即：DF2=FE2+FB2+FG2．应用这个定理尝试解决下列问题：已知图（2）是棱长为3cm的立方体，那么该立方体的对角线HB为    cm；连接BG，则△HBG的面积为    cm2．
【答案】分析：根据勾股定理，知对角线HB的平方即为棱长的平方的3倍；△HBG的面积即为HG•BG．
解答：解：连接HF．
根据勾股定理，得
HB===3（cm）；
△HBG的面积为HG•BG=×3×3=（cm2）．
点评：此题注意把立体中的有关计算转化为平面内的有关计算，熟练运用勾股定理．
练习册系列答案
相关题目
阅读理解题：
网格纸上画着纵、横两组平行线，相邻平行线之间的距离都相等，这两组平行线的交点称为格点，由多条线段首位顺次相接而组成的图形叫多边形，如果一个多边形的顶点都在格点上，那么这种多边形叫格点多边形，有趣的是：这种多边形的面积可根据图形内部及它的边上的格点数目来计算，算法十分简捷．
设格点多边形的面积为S，多边形内部的格点数为N，它边上的格点数为L，下面我们来探究S与N、L三者之间的数量关系，问题研究应从简单的图形入手．

（1）当N=0时的格点多边形，根据图1观察下表，填空：
图形序号    S    N    L
   ①    1    0    4
   ②    2    0    6
   ③    3    0    8
观察图1①、②、③可以发现S与L之间的数量关系式是：
S=
1
2
L-1
S=
1
2
L-1
；

（2）根据图2，填写下表：
图形序号    S    N    L  
1
2
  L
   ①    2.5       5    2.5
   ②       2    6    3
   ③    4    3     
请你在图2④的位置上再画一个N=2的格点多边形（不同于图2②）；
（3）综上分析与归纳，格点多边形的面积S与多边形内部的格点数N，它边上的格点数L之间的数量关系式是：
S=
1
2
L+N-1
S=
1
2
L+N-1
．
阅读理解题：网格纸上画着纵、横两组平行线，相邻平行线之间的距离都相等，这两组平行线的交点称为格点，由多条线段首尾顺次相接而组成的图形叫多边形，如果一个多边形的顶点都在格点上，那么这种多边形叫格点多边形，有趣的是：这种多边形的面积可根据图形内部及它的边上的格点数目来计算，算法十分简捷．设格点多边形的面积为S，多边形内部的格点数为N，它边上的格点数为L，下面我们来探究S与N、L三者之间的数量关系，问题研究应从简单的图形入手．
（1）当N=0时的格点多边形，根据图1观察下表，填空：
观察图1①、②、③可以发现S与L之间的数量关系式是：__________；
（2）根据图2，填写下表：
请你在图2④的位置上再画一个N=2的格点多边形（不同于图2②）；
（3）综上分析与归纳，格点多边形的面积S与多边形内部的格点数N，它边上的格点数L之间的数量关系式是：__________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网