题目内容
6.先化简,再求值:已知a=8,b=2,试求a$\sqrt{\frac{1}{a}}$+$\sqrt{4b}$-$\sqrt{\frac{a}{4}}$+$\sqrt{b}$的值.分析 先把二次根式化成最简二次根式,然后合并同类二次根式,再代入求值.
解答 解:a$\sqrt{\frac{1}{a}}$+$\sqrt{4b}$-$\sqrt{\frac{a}{4}}$+$\sqrt{b}$
=$\sqrt{a}$+2$\sqrt{b}$-$\frac{\sqrt{a}}{2}$+$\sqrt{b}$
=$\frac{\sqrt{a}}{2}$+3$\sqrt{b}$
当a=8,b=2时,
原式=$\frac{\sqrt{8}}{2}$+3$\sqrt{2}$
=$\sqrt{2}$+3$\sqrt{2}$
=4$\sqrt{2}$
点评 本题主要考查了二次根式的化简求值.注意若被开方数中含有分母,开出来后仍然充当分母.

练习册系列答案
相关题目
16.计算a8•a4的结果,正确的是( )
| A. | a4 | B. | a2 | C. | a32 | D. | a12 |
1.|-$\frac{3}{4}$|的相反数是( )
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
11.-$\frac{5}{6}$的相反数的倒数是( )
| A. | $\frac{5}{6}$ | B. | -$\frac{6}{5}$ | C. | $\frac{6}{5}$ | D. | -$\frac{5}{6}$ |
15.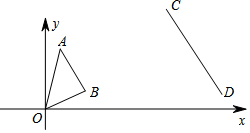 如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
 如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )| A. | (0,0) | B. | (3,4)或(-6,2) | C. | (5,3)或(-7,1) | D. | 不能确定 |
 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下: