题目内容
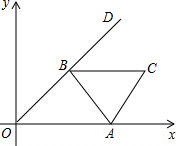 边长为2的等边△ABC的顶点A在x轴的正半轴上移动,顶点B在射线OD上移动,∠AOD=45°,则顶点C到原点O的最大距离为________.
边长为2的等边△ABC的顶点A在x轴的正半轴上移动,顶点B在射线OD上移动,∠AOD=45°,则顶点C到原点O的最大距离为________.
1+ +
+
分析:连接OC,当OC垂直平分AB时,线段OC的长最大,在两个直角三角形△ACE和△AOE中进行计算求出OC的长.
解答: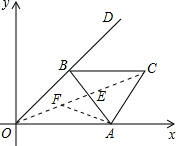 解:如图:
解:如图:
连接OC,当OC垂直平分AB时,OC最大.
此时∠ACO=30°,∠AOC=22.5°.
在直角△ACE中,CE=AC•sin60°=2× =
= .AE=AC•cos60°=2×
.AE=AC•cos60°=2× =1.
=1.
在直角△AOE中,∠AOE=22.5°,∠OAE=67.5°,
在EO上截取EF=EA=1,连接AF,则△AEF是等腰直角三角形,
∴AF= ,∠EAF=45°,
,∠EAF=45°,
∴∠FAO=22.5°=∠FOA.
∴FO=FA= ,
,
∴OC=OF+FE+EC= +1+
+1+ .
.
故答案是:1+ +
+ .
.
点评:本题考查的是解直角三角形,在直角△ACE中,用余弦求出CE的长,在直角△AOE中,根据两个锐角的关系,在较长直角边上截取较短的直角边长,根据等腰直角三角形以及等边对等角求出OE的长,然后得到OC的值.
 +
+
分析:连接OC,当OC垂直平分AB时,线段OC的长最大,在两个直角三角形△ACE和△AOE中进行计算求出OC的长.
解答:
 解:如图:
解:如图:连接OC,当OC垂直平分AB时,OC最大.
此时∠ACO=30°,∠AOC=22.5°.
在直角△ACE中,CE=AC•sin60°=2×
 =
= .AE=AC•cos60°=2×
.AE=AC•cos60°=2× =1.
=1.在直角△AOE中,∠AOE=22.5°,∠OAE=67.5°,
在EO上截取EF=EA=1,连接AF,则△AEF是等腰直角三角形,
∴AF=
 ,∠EAF=45°,
,∠EAF=45°,∴∠FAO=22.5°=∠FOA.
∴FO=FA=
 ,
,∴OC=OF+FE+EC=
 +1+
+1+ .
.故答案是:1+
 +
+ .
.点评:本题考查的是解直角三角形,在直角△ACE中,用余弦求出CE的长,在直角△AOE中,根据两个锐角的关系,在较长直角边上截取较短的直角边长,根据等腰直角三角形以及等边对等角求出OE的长,然后得到OC的值.

练习册系列答案
相关题目
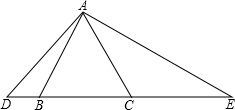 如图,△ABC是一个边长为2的等边三角形,D、E都在直线BC上,并且∠DAE=120°
如图,△ABC是一个边长为2的等边三角形,D、E都在直线BC上,并且∠DAE=120° △ABC是边长为2的等边三角形,点P、Q分别从A、C两点同时出发做匀速直线运动,且它们的速度相等.已知点P沿边射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC,垂足是E.
△ABC是边长为2的等边三角形,点P、Q分别从A、C两点同时出发做匀速直线运动,且它们的速度相等.已知点P沿边射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC,垂足是E. 过边长为2的等边△ABC的边AB上一点P,作PE⊥AC于点E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC边于点D,求DE的长.
过边长为2的等边△ABC的边AB上一点P,作PE⊥AC于点E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC边于点D,求DE的长. B.
B. C.
C. D.不能确定
D.不能确定

 B.
B. C.
C. D.不能确定
D.不能确定