题目内容
 如图,在一次夏令营活动中,小霞同学从营地A点出发,要到C地去,先沿北偏东70°方向到达B地,然后再沿北偏西20°的方向走到了目的地C,此时小霞在营地A的北偏东40°的方向上,则∠ACB的度数为
如图,在一次夏令营活动中,小霞同学从营地A点出发,要到C地去,先沿北偏东70°方向到达B地,然后再沿北偏西20°的方向走到了目的地C,此时小霞在营地A的北偏东40°的方向上,则∠ACB的度数为
- A.30°
- B.40°
- C.60°
- D.70°
C
分析:由题意可知,∠NAB,∠CBE,∠NAC,再结合角的和差求出∠CAB的度数,根据两直线平行同旁内角互补求∠ABC的度数,最后根据三角形的内角和求∠ACB的度数.
解答: 解:由题意可知,∠NAB=70°,∠CBE=20°,∠NAC=40°,
解:由题意可知,∠NAB=70°,∠CBE=20°,∠NAC=40°,
∴∠CAB=∠NAB-∠NAC=70°-40°=30°,
∵NA∥BE,
∴∠ABC=180°-∠NAB-∠CBE=90°,
∴∠ACB=180°-∠CAB-∠ABC=180°-30°-90°=60°.
故选C.
点评:解答此类题需要从运动的角度,根据方位角的度数,再结合三角形的内角和与平行线的性质求解.
分析:由题意可知,∠NAB,∠CBE,∠NAC,再结合角的和差求出∠CAB的度数,根据两直线平行同旁内角互补求∠ABC的度数,最后根据三角形的内角和求∠ACB的度数.
解答:
 解:由题意可知,∠NAB=70°,∠CBE=20°,∠NAC=40°,
解:由题意可知,∠NAB=70°,∠CBE=20°,∠NAC=40°,∴∠CAB=∠NAB-∠NAC=70°-40°=30°,
∵NA∥BE,
∴∠ABC=180°-∠NAB-∠CBE=90°,
∴∠ACB=180°-∠CAB-∠ABC=180°-30°-90°=60°.
故选C.
点评:解答此类题需要从运动的角度,根据方位角的度数,再结合三角形的内角和与平行线的性质求解.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 12、如图,在一次夏令营活动中,小霞同学从营地A点出发,要到C地去,先沿北偏东70°方向到达B地,然后再沿北偏西20°的方向走到了目的地C,此时小霞在营地A的北偏东40°的方向上,则∠ACB的度数为( )
12、如图,在一次夏令营活动中,小霞同学从营地A点出发,要到C地去,先沿北偏东70°方向到达B地,然后再沿北偏西20°的方向走到了目的地C,此时小霞在营地A的北偏东40°的方向上,则∠ACB的度数为( )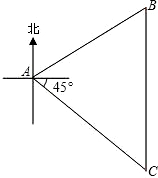 如图,在一次夏令营活动中,小明从A地出发,沿北偏东某个方向走500米到达B地;小红从A地出发,沿东南方向走400
如图,在一次夏令营活动中,小明从A地出发,沿北偏东某个方向走500米到达B地;小红从A地出发,沿东南方向走400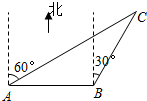 如图,在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了180m到达B地,再沿北偏东30°方向走,恰能到达目的地C,那么,由此可知,B、C两地相距
如图,在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了180m到达B地,再沿北偏东30°方向走,恰能到达目的地C,那么,由此可知,B、C两地相距 如图,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了500
如图,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了500 如图,在一次夏令营活动中,小明从A地出发,沿北偏东某个方向走500米到达B地;小红从A地出发,沿东南方向走400
如图,在一次夏令营活动中,小明从A地出发,沿北偏东某个方向走500米到达B地;小红从A地出发,沿东南方向走400 米到达C地.若C地恰好在B地的正南方向,求B、C两地之间的距离.
米到达C地.若C地恰好在B地的正南方向,求B、C两地之间的距离.