题目内容
 如图,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了500
如图,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了500| 3 |
分析:根据BE∥AD,得出∠DAB=∠ABE=60°,再根据平角的定义得出30°+∠CBA+∠ABE=180°,求出∠CBA的度数,判断出△ABC是直角三角形,最后根据勾股定理求出AC的值即可.
解答: 解:∵BE∥AD,
解:∵BE∥AD,
∴∠DAB=∠ABE=60°,
∵30°+∠CBA+∠ABE=180°,
∴∠CBA=90°,
∴△ABC为直角三角形,
∵BC=500,AB=500
,
∴AC2=BC2+AB2,
∴AC=
=1000(m).
答:A、C两点间的距离是1000m.
 解:∵BE∥AD,
解:∵BE∥AD,∴∠DAB=∠ABE=60°,
∵30°+∠CBA+∠ABE=180°,
∴∠CBA=90°,
∴△ABC为直角三角形,
∵BC=500,AB=500
| 3 |
∴AC2=BC2+AB2,
∴AC=
5002+(500
|
答:A、C两点间的距离是1000m.
点评:本题考查了方向角解直角三角形的应用,解题的关键是根据题意得出△ABC为直角三角形,再根据勾股定理求出AC的长.

练习册系列答案
相关题目
 12、如图,在一次夏令营活动中,小霞同学从营地A点出发,要到C地去,先沿北偏东70°方向到达B地,然后再沿北偏西20°的方向走到了目的地C,此时小霞在营地A的北偏东40°的方向上,则∠ACB的度数为( )
12、如图,在一次夏令营活动中,小霞同学从营地A点出发,要到C地去,先沿北偏东70°方向到达B地,然后再沿北偏西20°的方向走到了目的地C,此时小霞在营地A的北偏东40°的方向上,则∠ACB的度数为( )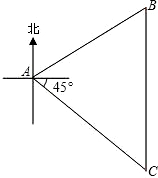 如图,在一次夏令营活动中,小明从A地出发,沿北偏东某个方向走500米到达B地;小红从A地出发,沿东南方向走400
如图,在一次夏令营活动中,小明从A地出发,沿北偏东某个方向走500米到达B地;小红从A地出发,沿东南方向走400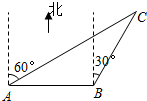 如图,在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了180m到达B地,再沿北偏东30°方向走,恰能到达目的地C,那么,由此可知,B、C两地相距
如图,在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了180m到达B地,再沿北偏东30°方向走,恰能到达目的地C,那么,由此可知,B、C两地相距 米到达C地.若C地恰好在B地的正南方向,求B、C两地之间的距离.
米到达C地.若C地恰好在B地的正南方向,求B、C两地之间的距离.