题目内容
 如图,圆心角为60°的扇形中,弦AB=6,则扇形面积为
如图,圆心角为60°的扇形中,弦AB=6,则扇形面积为
- A.π
- B.
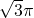
- C.6π
- D.12π
C
分析:过点C作CD⊥AB,垂足为D,根据垂径定理和勾股定理求得AC的长,从而得出扇形面积.
解答:过点C作CD⊥AB,垂足为D,
∵AB=6,∴AD=3,
∵∠C=60°,∴∠ACD=30°,
∴AC=6,
∴扇形面积 =6π,
=6π,
故选C.
点评:本题考查了扇形面积的计算,以及垂径定理和勾股定理,要熟练掌握.
分析:过点C作CD⊥AB,垂足为D,根据垂径定理和勾股定理求得AC的长,从而得出扇形面积.
解答:过点C作CD⊥AB,垂足为D,
∵AB=6,∴AD=3,
∵∠C=60°,∴∠ACD=30°,
∴AC=6,
∴扇形面积
 =6π,
=6π,故选C.
点评:本题考查了扇形面积的计算,以及垂径定理和勾股定理,要熟练掌握.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 如图,圆心角为60°的扇形中,弦AB=6,则扇形面积为( )
如图,圆心角为60°的扇形中,弦AB=6,则扇形面积为( )| A、π | ||
B、
| ||
| C、6π | ||
| D、12π |





