Question

如图，在Rt △ ABC 中，∠C="90°" ，AC=BC=4cm，点P从点A出发，沿AB方向以每秒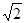cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，将△PQC沿BC翻折，点P的对应点为点P′.设Q点运动的时间t秒，若四边形QPCP′为菱形，则t的值为_________．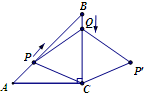

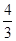
Answer 1

解析试题分析：首先连接PP′交BC于O，根据菱形的性质可得PP′⊥CQ，可证出PO∥AC，根据平行线分线段成比例可得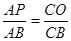，再表示出AP、AB、CO的长，代入比例式可以算出t的值．
连接PP′交BC于O，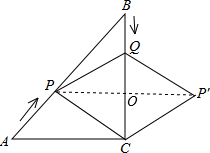

∵若四边形QPCP′为菱形，
∴PP′⊥QC，
∴∠POQ=90°，
∵∠C=90°，
∴PO∥AC，
∴，
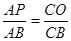∵设点Q运动的时间为t秒，
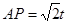∴，QB=t，
∴QC=4-t，
∴
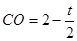
∵AC=CB=4，∠ACB=90°，
∴
∴
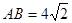
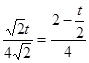
解得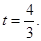
考点：菱形的性质，勾股定理，平行线分线段成比例
点评：解答本题的关键是熟记平行线分线段成比例定理的推论：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．