题目内容
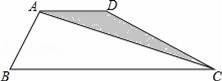
如图,△ABC中,∠A=60°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DE的度数为 .


65° .
【考点】翻折变换(折叠问题).
【专题】几何图形问题.
【分析】首先求得∠AEA′,根据折叠的性质可得∠A′ED=∠AED=
 ∠AEA′,在△A′DE中利用三角形内角和定理即可求解.
∠AEA′,在△A′DE中利用三角形内角和定理即可求解.
【解答】解:∵∠AEA′=180°﹣∠A′EC=180°﹣70°=110°,
又∵∠A′ED=∠AED=
 ∠AEA′=55°,∠DA′E=∠A=60°,
∠AEA′=55°,∠DA′E=∠A=60°,
∴∠A′DE=180°﹣∠A′ED﹣∠DA′E=180°﹣55°﹣60°=65°.
故答案为:65°.
【点评】本题考查了折叠的性质,找出图形中相等的角和相等的线段是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为增强环境保护意识,争创“文明卫生城市”,某企业对职工进行了一次“生产和居住环境满意度”的调查,按年龄分组,得到下面的各组人数统计表:
各组人数统计表
| 组号 | 年龄分组 | 频数(人) | 频率 |
| 第一组 | 20≤x<25 | 50 | 0.05 |
| 第二组 | 25≤x<30 | a | 0.35 |
| 第三组 | 30≤x<35 | 300 | 0.3 |
| 第四组 | 35≤x<40 | 200 | b |
| 第五组 | 40≤x≤45 | 100 | 0.1 |
(1)求本次调查的样本容量及表中的a、b的值;
(2)调查结果得到对生产和居住环境满意的人数的频率分布直方图如图所示.政策规定:本次调查满意人数超过调查人数的一半,则称调查结果为满意.如果第一组满意人数为36,请问此次调查结果是否满意;并指出第五组满意人数的百分比;
(3)从第二组和第四组对生产和居住环境满意的职工中分别抽取3人和2人作义务宣传员,在这5人中随机抽取2人介绍经验,求第二组和第四组恰好各有1人被抽中介绍经验的概率.







 B.
B.
 C.
C.






 B.
B. C.
C. D.
D.