��Ŀ����
Ϊ��ǿ����������ʶ�������������������С���ij��ҵ��ְ��������һ�Ρ������;�ס��������ȡ��ĵ��飬��������飬�õ�����ĸ�������ͳ�Ʊ���
��������ͳ�Ʊ�
| ��� | ������� | Ƶ�����ˣ� | Ƶ�� |
| ��һ�� | 20��x��25 | 50 | 0.05 |
| �ڶ��� | 25��x��30 | a | 0.35 |
| ������ | 30��x��35 | 300 | 0.3 |
| ������ | 35��x��40 | 200 | b |
| ������ | 40��x��45 | 100 | 0.1 |
��1���ε�����������������е�a��b��ֵ��
��2���������õ��������;�ס���������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����߹涨�����ε�������������������������һ�룬��Ƶ�����Ϊ���⣮�����һ����������Ϊ36�����ʴ˴ε������Ƿ����⣻��ָ�����������������İٷֱȣ�
��3���ӵڶ���͵�����������;�ס���������ְ���зֱ��ȡ3�˺�2������������Ա������5���������ȡ2�˽��ܾ��飬��ڶ���͵�����ǡ�ø���1�˱����н��ܾ���ĸ��ʣ�


�����㡿Ƶ�����ʣ��ֲ�ֱ��ͼ��Ƶ�����ʣ��ֲ������б�������״ͼ����
��ר�⡿ͼ���ͣ�
����������1�����ݵ�һ���������50��Ƶ����0.05��������������������Ƶ�ʹ�ʽ�������a��b��ֵ��
��2�����ݵ�һ���Ƶ����36�ˣ�Ƶ����0.06�ݴ˼�����õ������������������Ⱥ͵��������������İٷֱȼ�����ã�
��3����A��ʾ�ӵڶ����ȡ���ˣ���B��ʾ�ӵ������ȡ���ˣ������оٷ�������⣮
����𡿽⣺��1���������������50��0.05=1000���ˣ���
��a=1000��0.35=350��
b=
 =0.2��
=0.2��
������������Ϊ1000��
��2��������������ǣ�36��0.06=600���ˣ���
�������������ǣ�
 =0.6����˴ε�����Ϊ���⣻
=0.6����˴ε�����Ϊ���⣻
�����������������ǣ�600��0.16=96���ˣ���
���������������ǣ�
 ��100%=96%��
��100%=96%��
��3����A��ʾ�ӵڶ����ȡ���ˣ���B��ʾ�ӵ������ȡ���ˣ�

 ��
��
�ܹ���20���������ڶ���͵�����ǡ�ø���1�˱����еĸ����ǣ�
 =
=
 ��
��
�����������⿼���Ƶ���ֲ�ֱ��ͼ������������ͳ��ͼ��ȡ��Ϣ������������ͳ��ͼ��ȡ��Ϣʱ����������۲졢�������о�ͳ��ͼ������������ȷ���жϺͽ�����⣮

 ��У����ϵ�д�
��У����ϵ�д� ﹣
﹣ +|﹣2|﹣��﹣2��2
+|﹣2|﹣��﹣2��2




 B��
B��



 =
=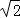 ﹣1��
﹣1�� =
= ��
�� =2﹣
=2﹣ ���������㷢�ֵĹ��ɼ��㣺
���������㷢�ֵĹ��ɼ��㣺 +��+
+��+ ������
������ +
+ ��=__________��
��=__________��