题目内容
20.已知△ABC和△A′B′C′中,$\frac{AB}{A′B′}=\frac{BC}{B′C′}=\frac{CA}{C′A′}=\frac{2}{3}$,且A′B′+B′C′+C′A′=24cm,求△ABC的周长.分析 根据相似三角形的判定和性质即可得到结论.
解答 解:∵$\frac{AB}{A′B′}=\frac{BC}{B′C′}=\frac{CA}{C′A′}=\frac{2}{3}$,
∴△ABC∽△A′B′C′,
∴△ABC的周长:△A′B′C′的周长=$\frac{2}{3}$,
∵A′B′+B′C′+C′A′=24cm,
∴△ABC的周长=16cm.
点评 本题考查了相似三角形的判定和性质,知道相似三角形的周长的比相等相似比是解题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
10.下列各数:$\frac{π}{2}$,0,$\sqrt{9}$,$\frac{1}{2}$,$0.\stackrel{••}{23}$,$\frac{22}{7}$,0.30003000…,1-$\sqrt{2}$中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
8.已知三角形两个内角的差等于第三个内角,则它是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等边三角形 |
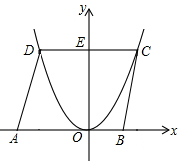 如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成平行四边形ABCD,DC与y轴的交点为E(0,6),试求a的值.
如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成平行四边形ABCD,DC与y轴的交点为E(0,6),试求a的值. 如图,在△ABC中,BC=4.5,PM、QN分别垂直平分AB和AC,则△PAQ的周长等于4.5.
如图,在△ABC中,BC=4.5,PM、QN分别垂直平分AB和AC,则△PAQ的周长等于4.5.