题目内容
如图，在△ABC中，过AB边上的一点M作MN∥BC交AC于点N，使得△ANM的面积与梯形MNCB的面积之比为4：5，连接BN，MC交于点G，己知△BGC的面积为1，则△ABC的面积等于（ ）| A、3 | ||
| B、4 | ||
| C、5 | ||
D、
|
考点：面积及等积变换
专题：
分析：根据平行线得出三角形相似，推出
=
=
=
，根据三角形面积公式求出△BGM和△CGN的面积，根据相似三角形的面积比等于相似比的平方求出△MNG的面积，求出四边形MNCB的面积，最后根据相似三角形的面积比等于相似比求出△ABC的面积即可．
| MN |
| BC |
| 2 |
| 3 |
| NG |
| BG |
| MG |
| CG |
解答：解：∵MN∥BC，
∴△AMN∽△ABC，△MNG∽△CBG，
∴
=
=
=
，
∵△ANM的面积与梯形MNCB的面积之比为4：5，
∴△AMN的面积与△ABC的面积比为4：9，
∴
=
=
=
，
∵△BGC的面积为1，且△BGC边BG上的高和△CGN边NG上的高相等，
∴
=
=
，
∴S△CGN=
，
同理S△MNG=
，
∵△MNG∽△CBG，相似比是2：3，
∴
=
，
∴S△MNG=
，
∴四边形MNCB的面积是1+
+
+
=
，
设△ABC的面积是S，
∵△AMN∽△ABC，相似比是2：3，
∴
=
，
∴
=
，
解得：S=5，
故选C．
∴△AMN∽△ABC，△MNG∽△CBG，
∴
| MN |
| BC |
| AM |
| AB |
| NG |
| BG |
| MG |
| CG |
∵△ANM的面积与梯形MNCB的面积之比为4：5，
∴△AMN的面积与△ABC的面积比为4：9，
∴
| MN |
| BC |
| 2 |
| 3 |
| NG |
| BG |
| MG |
| CG |
∵△BGC的面积为1，且△BGC边BG上的高和△CGN边NG上的高相等，
∴
| S△CGN |
| S△BCG |
| NG |
| BG |
| 2 |
| 3 |
∴S△CGN=
| 2 |
| 3 |
同理S△MNG=
| 2 |
| 3 |
∵△MNG∽△CBG，相似比是2：3，
∴
| S△MNG |
| S△CBG |
| 4 |
| 9 |
∴S△MNG=
| 4 |
| 9 |
∴四边形MNCB的面积是1+
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 25 |
| 9 |
设△ABC的面积是S，
∵△AMN∽△ABC，相似比是2：3，
∴
| S△AMN |
| S△ABC |
| 4 |
| 9 |
∴
S-
| ||
| S |
| 4 |
| 9 |
解得：S=5，
故选C．
点评：本题考查了相似三角形的性质和判定和三角形面积公式得灵活运用，关键是灵活运用相似三角形的面积比等于相似比和三角形的面积公式进计算，题目比较好，是一道具有一定代表性的题目．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC内接于⊙O，AD是BC边上的高，AO的延长线交⊙O于点E．已知AB=| 6 |
| 3 |
A、3
| ||
B、2
| ||
C、3
| ||
D、2
|
如图，桌面上放着两个物体，按下图所示的方式摆放在一起，其左视图是（ ）A、 |
B、 |
C、 |
D、 |
如图，正方形ABCD的面积是120平方厘米，E是AB的中点，F是BC的中点，四边形BGHF的面积是多少平方厘米？
用15个
字形纸片和1个
字纸片，能否盖满1个8×8方格棋盘．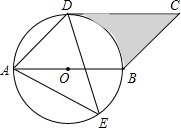
如图，四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，E是⊙O上一点，且∠AED=45°．