题目内容
已知a+b=tan20°，则函数y=
(x＜0)的图象在（ ）
| -a-b |
| x |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
分析：根据三角函数确定a+b=tan20°＞0，再根据反比例函数图象的性质进行解答即可．
解答：解：∵a+b=tan20°＞0，
∴-a-b＜0，
∴反比例函数图象位于第二四象限，
又∵x＜0，
∴函数图象位于第二象限．
故选B．
∴-a-b＜0，
∴反比例函数图象位于第二四象限，
又∵x＜0，
∴函数图象位于第二象限．
故选B．
点评：本题主要考查了反比例函数的性质，比例系数：k＞0时，反比例函数图象位于第一、三象限，k＜0时，反比例函数图象位于第二、四象限，根据锐角三角函数确定出a+b＞0是解题的关键．
练习册系列答案
优学名师名题系列答案
相关题目
如图，挂着“庆祝海门实验学校建校三周年”条幅的氢气球升在校园上空，已知气球的直径为4m，在地面A点测得气球中心O的仰角为∠OAD=60°，测得气球的视角∠BAC=2°（AB、AC为⊙O的切线，B、C为切点）．则气球中心O离地面的高度OD约为多少？已知AB和CD分别是半圆O的直径和弦，AD和BC的夹角为ａ，则S△CDE: S△ABE等于（ ）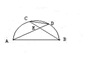 
| A．Sin2ａ | B．cos2ａ | C．tan2ａ | D． sinａ |
