题目内容
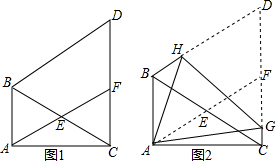
18. 如图,在△ABC中,AB=AC,将△ABC绕点A逆时针旋转得到△ADE,连接BD、CE,BD,CE相交于点F,且∠ADB=∠DAE.
如图,在△ABC中,AB=AC,将△ABC绕点A逆时针旋转得到△ADE,连接BD、CE,BD,CE相交于点F,且∠ADB=∠DAE.(1)求证:AD2=BO•BD;
(2)求证:四边形ABFE为菱形.
分析 (1)由旋转的性质得出AD=AB,AE=AC,∠DAE=∠BAC,证出∠BAC=∠ADB,再由∠ABO=∠DBA,得出△ABO∽△DBA,得出对应边成比例证出AB2=BO•BD,即可得出结论;
(2)由旋转的性质得出AD=AB,AE=AC,∠DAE=∠BAC,得出∠ABD=∠ADB,∠ACE=∠AEC,∠BAD=∠CAE,证出∠DAE=∠ADB,得出AE∥BD,由三角形内角和定理证出∠ABD=∠ACE,得出∠BAC=∠ACE,证出AB∥CE,得出四边形ABFE是平行四边形,即可得出结论.
解答 (1)证明:由旋转的性质得:△ADE≌△ABC,
∴AD=AB,AE=AC,∠DAE=∠BAC,
∵∠ADB=∠DAE,
∴∠BAC=∠ADB,
又∵∠ABO=∠DBA,
∴△ABO∽△DBA,
∴$\frac{AB}{BD}=\frac{BO}{AB}$,
∴AB2=BO•BD,
∴AD2=BO•BD;
(2)证明:由旋转的性质得:△ADE≌△ABC,
∴AD=AB,AE=AC,∠DAE=∠BAC,
∴∠ABD=∠ADB,∠ACE=∠AEC,∠BAD=∠CAE,
∵AB=AC,
∴AB=AE,
∵∠ADB=∠DAE,
∴AE∥BD,
∵∠BAD+∠ABD+∠ADB=180°,∠CAE+∠ACE+∠AEC=180°,
∴∠ABD=∠ACE,
∴∠BAC=∠ACE,
∴AB∥CE,
∴四边形ABFE是平行四边形,
又∵AB=AE,
∴四边形ABFE为菱形.
点评 本题考查了旋转的性质、平行四边形的判定方法、菱形的判定方法、等腰三角形的性质、平行线的判定方法;熟练掌握旋转的性质,证明四边形是平行四边形是解决问题的关键,有一定难度.

练习册系列答案
相关题目

 如图,春节来临,小明约同学周末去文化广场放风筝,他放的风筝线AE长为115m,他的风筝线(近似地看作直线)与水平地面构成42°角,若小明身高AB为1.42m,求他的风筝飞的高度CF(精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
如图,春节来临,小明约同学周末去文化广场放风筝,他放的风筝线AE长为115m,他的风筝线(近似地看作直线)与水平地面构成42°角,若小明身高AB为1.42m,求他的风筝飞的高度CF(精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
 图中的四边形均为矩形.根据图形,写出一个正确的等式:(m+a)(m+b)=m2+am+bm+ab(答案不唯一).
图中的四边形均为矩形.根据图形,写出一个正确的等式:(m+a)(m+b)=m2+am+bm+ab(答案不唯一).