题目内容
5.在下列命题:①若$\widehat{AB}$=$\widehat{CD}$,则AB=CD;
②若$\widehat{AB}$=2$\widehat{CD}$,则AB=2CD;
③圆心角∠AOB等于圆心角∠COD,则AB=CD;
④在⊙O上任意分布的四个点A、B、C、D,则∠ABC+∠ADC=180°,
其中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 分别利用圆周角定理以及圆内接四边形的性质分别分析得出即可.
解答 解:①若$\widehat{AB}$=$\widehat{CD}$,则AB=CD,正确;
②若$\widehat{AB}$=2$\widehat{CD}$,则AB=2CD,错误;
③在同圆或等圆中,圆心角∠AOB等于圆心角∠COD,则AB=CD,故错误;
④在⊙O上任意分布的四个点A、B、C、D,则∠ABC+∠ADC=180°,正确,
故选:B.
点评 此题主要考查了命题与定理,正确把握相关性质是解题关键.

练习册系列答案
相关题目
10.已知m=x+1,n=-x+2,若规定y=$\left\{\begin{array}{l}{1+m-n,m≥n}\\{1-m+n,m<n}\end{array}\right.$,则y的最小值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
20.若等腰三角形腰长为10cm,底边长为16cm,那么它的面积为( )
| A. | 48cm2 | B. | 36cm2 | C. | 24cm2 | D. | 12cm2 |
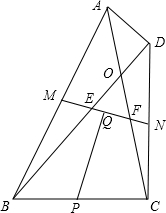 如图,在四边形ABCD中,对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点.
如图,在四边形ABCD中,对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点. 如图,一次函数y=kx+b(k≠0)的图象如图所示,在第一象限内的图象上是否存在一定P,使过点P所作的两坐标轴的垂线与两坐标轴围成的四边形的面积为2?若存在,求出点P的坐标;若不存在,请说明理由.
如图,一次函数y=kx+b(k≠0)的图象如图所示,在第一象限内的图象上是否存在一定P,使过点P所作的两坐标轴的垂线与两坐标轴围成的四边形的面积为2?若存在,求出点P的坐标;若不存在,请说明理由. 如图是一数值转换机,若输入的x为-3,则输出的结果为15.
如图是一数值转换机,若输入的x为-3,则输出的结果为15. 如图,已知直角坐标系中A(-1,4)、B(0,2),平移线段AB,使点B移到点C(3,0),此时点A记作点D,则四边形ABCD的面积是5.
如图,已知直角坐标系中A(-1,4)、B(0,2),平移线段AB,使点B移到点C(3,0),此时点A记作点D,则四边形ABCD的面积是5.