题目内容
10. 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则等边△ABC的边长为9.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则等边△ABC的边长为9.
分析 由∠ADE=60°,可证得△ABD∽△DCE;可用等边三角形的边长表示出DC的长,进而根据相似三角形的对应边成比例,求得△ABC的边长.
解答 解:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=BC;
∴CD=BC-BD=AB-3;
∴∠BAD+∠ADB=120°
∵∠ADE=60°,
∴∠ADB+∠EDC=120°,
∴∠DAB=∠EDC,
又∵∠B=∠C=60°,
∴△ABD∽△DCE;
∴$\frac{AB}{CD}$=$\frac{BD}{CE}$,即$\frac{AB}{AB-3}$=$\frac{3}{2}$,
解得AB=9.
故答案为:9.
点评 此题主要考查了等边三角形的性质和相似三角形的判定和性质,能够证得△ABD∽△DCE是解答此题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.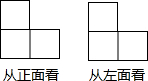 如图,是由若干个完全相同的小正方体组成的一个几何体的从正面看和从左面看的图形,则组成这个几何体的小正方体的个数是( )
如图,是由若干个完全相同的小正方体组成的一个几何体的从正面看和从左面看的图形,则组成这个几何体的小正方体的个数是( )
 如图,是由若干个完全相同的小正方体组成的一个几何体的从正面看和从左面看的图形,则组成这个几何体的小正方体的个数是( )
如图,是由若干个完全相同的小正方体组成的一个几何体的从正面看和从左面看的图形,则组成这个几何体的小正方体的个数是( )| A. | 3个或4个或5个 | B. | 4个或5个 | C. | 5个或6个 | D. | 6个或7个 |
5.方程x-$\frac{x-5}{3}$=1,去分母得( )
| A. | 3x-2x+10=1 | B. | x-(x-5)=3 | C. | 3x-(x-5)=3 | D. | 3x-2x+10=6 |
15.点A在平面直角坐标系中的第二象限,且A点到x轴的距离为3,到y轴的距离为5,则A的坐标为( )
| A. | (-5,3) | B. | (-3,5) | C. | (5,-3) | D. | (3,-5) |
2.以下四组木棒中,哪一组的三条能够刚好做成直角三角形的木架( )
| A. | 7厘米,12厘米,15厘米 | B. | 7厘米,12厘米,13厘米 | ||
| C. | 8厘米,15厘米,16厘米 | D. | 3厘米,4厘米,5厘米 |
19.点A在直角坐标系中的坐标是(3,4),则点A到x轴和y轴的距离分别是( )
| A. | 3,4 | B. | 3,4 | C. | 4,3 | D. | 4,3 |
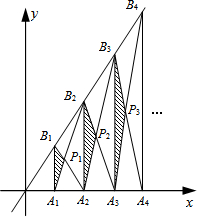 已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=2x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2 B3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn.若△A1B1P1,△A2B2P2,△A3B3P3,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn为$\frac{{n}^{2}}{2n+1}$.
已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=2x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2 B3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn.若△A1B1P1,△A2B2P2,△A3B3P3,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn为$\frac{{n}^{2}}{2n+1}$. 如图,小明为了测量河的宽度,在河岸同侧取了点C,B,A,在点C处测得对岸一棵树P在正北方向,经过测量得知:∠PBC=45°,∠PAC=30°,AB=10米,由此小明计算出河的宽度为5$\sqrt{3}$+5米(结果保留根号).
如图,小明为了测量河的宽度,在河岸同侧取了点C,B,A,在点C处测得对岸一棵树P在正北方向,经过测量得知:∠PBC=45°,∠PAC=30°,AB=10米,由此小明计算出河的宽度为5$\sqrt{3}$+5米(结果保留根号). 如图,在△ABC中,AB=BC,点E在边AB上,EF⊥AC于F.
如图,在△ABC中,AB=BC,点E在边AB上,EF⊥AC于F.