题目内容
(2012•宜宾)为了解学生的艺术特长发展情况,某校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.

请你根据统计图解答下列问题:
(1)在这次调查中一共抽查了
(2)若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率.

请你根据统计图解答下列问题:
(1)在这次调查中一共抽查了
50
50
名学生,其中,喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为24%
24%
,喜欢“戏曲”活动项目的人数是4
4
人;(2)若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率.
分析:(1)总人数=参加某项的人数÷所占比例,用喜欢“舞蹈”活动项目的人数除以总人数再乘100%,即可求出喜欢“舞蹈”活动项目的人数占抽查总人数的百分比,用总人数减去其他4个小组的人数求出喜欢“戏曲”活动项目的人数;
(2)根据频率的计算方法,用选中“舞蹈、声乐”这两项活动的数除以总数计算即可解答.
(2)根据频率的计算方法,用选中“舞蹈、声乐”这两项活动的数除以总数计算即可解答.
解答:解:(1)根据喜欢声乐的人数为8人,得出总人数=8÷16%=50,
喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为:
×100%=24%,
喜欢“戏曲”活动项目的人数是:50-12-16-8-10=4,
故答案为:50,24%,4;
(2)(用树状图)设舞蹈、乐器、声乐、戏曲的序号依次是①②③④,

故恰好选中“舞蹈、声乐”两项活动的概率是
=
;
(用列表法)
故恰好选中“舞蹈、声乐”两项活动的概率是
=
.
喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为:
| 12 |
| 50 |
喜欢“戏曲”活动项目的人数是:50-12-16-8-10=4,
故答案为:50,24%,4;
(2)(用树状图)设舞蹈、乐器、声乐、戏曲的序号依次是①②③④,

故恰好选中“舞蹈、声乐”两项活动的概率是
| 2 |
| 12 |
| 1 |
| 6 |
(用列表法)
| 舞蹈 | 乐器 | 声乐 | 戏曲 | |
| 舞蹈 | 舞蹈、乐器 | 舞蹈、声乐 | 舞蹈、戏曲 | |
| 乐器 | 乐器、舞蹈 | 乐器、声乐 | 乐器、戏曲 | |
| 声乐 | 声乐、舞蹈 | 声乐、乐器 | 声乐、戏曲 | |
| 戏曲 | 戏曲、舞蹈 | 戏曲、乐器 | 戏曲、声乐 |
| 2 |
| 12 |
| 1 |
| 6 |
点评:本题主要考查条形统计图与扇形统计图的综合运用,用到的知识点为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.总体数目=部分数目÷相应百分比.
| m |
| n |

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
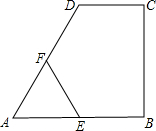 (2012•宜宾)如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=
(2012•宜宾)如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=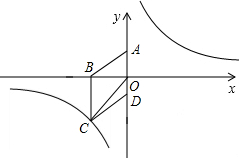 (2012•宜宾)如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).
(2012•宜宾)如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0). (2012•宜宾)如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为
(2012•宜宾)如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为