题目内容
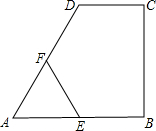 (2012•宜宾)如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=
(2012•宜宾)如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=| 1 |
| 2 |
分析:根据三角形的中位线求出EF=
BD,EF∥BD,推出△AEF∽△ABD,得出
=
,求出
=
=
,即可求出△AEF与多边形BCDFE的面积之比.
| 1 |
| 2 |
| S△AEF |
| S△ABD |
| 1 |
| 4 |
| S△CDB |
| S△ABD |
| ||
|
| 1 |
| 2 |
解答:解:连接BD,
∵F、E分别为AD、AB中点,
∴EF=
BD,EF∥BD,
∴△AEF∽△ABD,
∴
=(
)2=
,
∴△AEF的面积:四边形EFDB的面积=1:3,
∵CD=
AB,CB⊥DC,AB∥CD,
∴
=
=
,
∴△AEF与多边形BCDFE的面积之比为1:(1+4)=1:5,
故选C.

∵F、E分别为AD、AB中点,
∴EF=
| 1 |
| 2 |
∴△AEF∽△ABD,
∴
| S△AEF |
| S△ABD |
| EF |
| BD |
| 1 |
| 4 |
∴△AEF的面积:四边形EFDB的面积=1:3,
∵CD=
| 1 |
| 2 |
∴
| S△CDB |
| S△ABD |
| ||
|
| 1 |
| 2 |
∴△AEF与多边形BCDFE的面积之比为1:(1+4)=1:5,
故选C.
点评:本题考查了三角形的面积,三角形的中位线等知识点的应用,主要考查学生运用性质进行推理和计算的能力,题目比较典型,难度适中.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
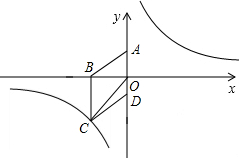 (2012•宜宾)如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).
(2012•宜宾)如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).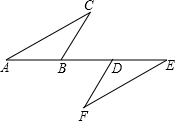 (2012•宜宾)如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.
(2012•宜宾)如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.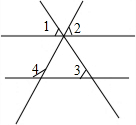 (2012•宜宾)如图,已知∠1=∠2=∠3=59°,则∠4=
(2012•宜宾)如图,已知∠1=∠2=∠3=59°,则∠4= (2012•宜宾)如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为
(2012•宜宾)如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为 (2012•宜宾)如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE=
(2012•宜宾)如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE=