题目内容
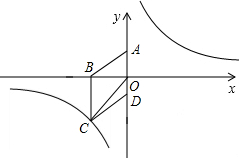 (2012•宜宾)如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).
(2012•宜宾)如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COD的面积相等.求点P的坐标.
分析:(1)根据菱形的性质可得菱形的边长,进而可得点C的坐标,代入反比例函数解析式可得所求的解析式;
(2)设出点P的坐标,易得△COD的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,就求得了点P的坐标.
(2)设出点P的坐标,易得△COD的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,就求得了点P的坐标.
解答:解:(1)由题意知,OA=3,OB=4
在Rt△AOB中,AB=
=5
∵四边形ABCD为菱形
∴AD=BC=AB=5,
∴C(-4,-5).
设经过点C的反比例函数的解析式为y=
(k≠0),
则
=-5,解得k=20.
故所求的反比例函数的解析式为y=
.
(2)设P(x,y)
∵AD=AB=5,OA=3,
∴OD=2,S△COD=
×2×4=4
即
•OA•|x|=4,
∴|x|=
,
∴x=±
当x=
时,y=
=
,当x=-
时,y=
=-
∴P(
,
)或(-
,-
).
在Rt△AOB中,AB=
| 32+42 |
∵四边形ABCD为菱形
∴AD=BC=AB=5,
∴C(-4,-5).
设经过点C的反比例函数的解析式为y=
| k |
| x |
则
| k |
| -4 |
故所求的反比例函数的解析式为y=
| 20 |
| x |
(2)设P(x,y)
∵AD=AB=5,OA=3,
∴OD=2,S△COD=
| 1 |
| 2 |
即
| 1 |
| 2 |
∴|x|=
| 8 |
| 3 |
∴x=±
| 8 |
| 3 |
当x=
| 8 |
| 3 |
| 20 | ||
|
| 15 |
| 2 |
| 8 |
| 3 |
| 20 | ||
-
|
| 15 |
| 2 |
∴P(
| 8 |
| 3 |
| 15 |
| 2 |
| 8 |
| 3 |
| 15 |
| 2 |
点评:综合考查反比例函数及菱形的性质,注意:根据菱形的性质得到点C的坐标;点P的横坐标的有两种情况.

练习册系列答案
相关题目
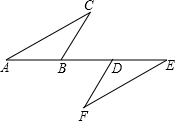 (2012•宜宾)如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.
(2012•宜宾)如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.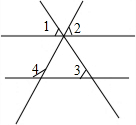 (2012•宜宾)如图,已知∠1=∠2=∠3=59°,则∠4=
(2012•宜宾)如图,已知∠1=∠2=∠3=59°,则∠4= (2012•宜宾)如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为
(2012•宜宾)如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为 (2012•宜宾)如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE=
(2012•宜宾)如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE=