题目内容
19.若关于x的不等式2(x-a)<a+6的解集和不等式2x-4<0的解集相同,求a.分析 根据解不等式的方法,可得不等式的解集,根据不等式的解集相同,可得关于a的方程,根据解方程,可得答案.
解答 解:解2(x-a)<a+6,得
x<$\frac{3a+6}{2}$.
解2x-4<0,得
x<2.
由关于x的不等式2(x-a)<a+6的解集和不等式2x-4<0的解集相同,得
$\frac{3a+6}{2}$=2.
解得a=-$\frac{2}{3}$.
点评 本题考查了不等式的解集,利用不等式的解集相同得出关于a的方程是解题关键.

练习册系列答案
相关题目
7.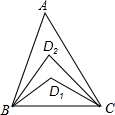 如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
 如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )| A. | 24° | B. | 25° | C. | 30° | D. | 36° |
14.若不等式组$\left\{\begin{array}{l}{\frac{1}{3}x>1}\\{2-x≥a}\end{array}\right.$无解,则a的取值范围是( )
| A. | a>3 | B. | a≥-1 | C. | -1≤a<3 | D. | a≤-1 |
11.在坐标平面上两点A(-a+2,-b+1)、B(3a,b),若点A向右移动2个单位长度后,再向下移动3个单位长度后与点B重合,则点B所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.某小区超市一段时间每天订购80个面包进行销售,每售出1个面包获利润0.5元,未售出的每个亏损0.3元.(1)若今后每天售出的面包个数用x(0<x≤80)表示,每天销售面包的利润用y(元)表示,写出y与x的函数关系式;
(2)小明连续m天对该超市的面包销量进行统计,并制成了频数分别直方图(每个组距包含左边的数,但不包含右边的数)和扇形统计图,如图1、图2所示,请结合两图提供的信息,解答下列问题:
①m的值为30;
②求在m天内日销售利润少于32元的天数;
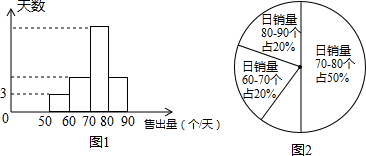
(3)如图(2)中m天内日销售面包个数在70≤x<80这个组内的销售情况如表:
请计算该组内平均每天销售面包的个数.
(2)小明连续m天对该超市的面包销量进行统计,并制成了频数分别直方图(每个组距包含左边的数,但不包含右边的数)和扇形统计图,如图1、图2所示,请结合两图提供的信息,解答下列问题:
①m的值为30;
②求在m天内日销售利润少于32元的天数;

(3)如图(2)中m天内日销售面包个数在70≤x<80这个组内的销售情况如表:
| 销售量/个 | 70 | 72 | 73 | 75 | 78 | 79 |
| 天数 | 1 | 2 | 3 | 4 | 3 | 2 |
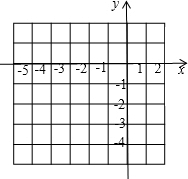 如图所示,已知△ABC是格点三角形
如图所示,已知△ABC是格点三角形