题目内容
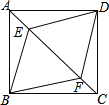
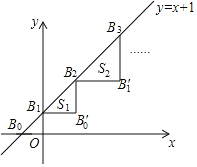
【题目】如图,直线y=x+1与x轴和y轴分别交于B0,B1两点,将B1B0绕B1逆时针旋转135°得B1B0′,过点B0'作y轴平行线,交直线y=x+1于点B2,记△B1B0B2的面积为S1;再将B2B1绕B2逆时针旋转135°得B2B1',过点B1'作y轴平行线,交直线y=x+l于点B3,记△B2B1'B3的面积为S2…以此类推,则△BnBn﹣1'Bn+1的面积为Sn=( )
A.(![]() )nB.(
)nB.(![]() )n﹣1C.2nD.2n﹣1
)n﹣1C.2nD.2n﹣1
【答案】D
【解析】
根据直线与x轴的成角和已知,可以判断∴△B1B0B2;…;△BnBn﹣1'Bn+1都是直角三角形,再由旋转的性质得到B1B0′=![]() OB0,B2B1′=
OB0,B2B1′=![]() B1B0′,…,Bn+1B′n=
B1B0′,…,Bn+1B′n=![]() BnBn﹣1′,可以B1B0′=
BnBn﹣1′,可以B1B0′=![]() ,B2B1′=2,…,BnBn﹣1'=
,B2B1′=2,…,BnBn﹣1'=![]() ,根据三角形面积公式即可求解.
,根据三角形面积公式即可求解.
解:直线l1:y=x+1与x轴正半轴夹角45°,
由题意可知B′0B1∥x轴,B1′B2∥x轴,…,Bn′Bn+1∥x轴,
B′0B2∥y轴,B′1B3∥y轴,…,B′n﹣1Bn+1∥y轴,
∴△B1B0B2;…;△BnBn﹣1'Bn+1都是直角三角形,
∴B1B0′=![]() OB0,B2B1′=
OB0,B2B1′=![]() B1B0′,…,Bn+1B′n=
B1B0′,…,Bn+1B′n=![]() BnBn﹣1′
BnBn﹣1′
由直线l1:y=x+1可知,B0(﹣1,0),B1(0,1),
∴OB0=1,
∴B1B0′=![]() ,B2B1′=2,…,BnBn﹣1'=
,B2B1′=2,…,BnBn﹣1'=![]() ,
,
∴△BnBn﹣1'Bn+1的面积为Sn=![]() (
(![]() )2=2n﹣1
)2=2n﹣1
故选:D.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】下面是“作一个![]() 角”的尺规作图过程.
角”的尺规作图过程.
已知:平面内一点A. 求作: |
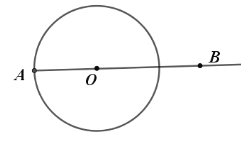
作法:如图,
①作射线 ②在射线 ③分别以 ④作射线 则 |
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:![]() ,
,
![]() ______
______![]() _______
_______![]() .
.
![]() _____
_____![]() .(_____________)(填推理的依据)
.(_____________)(填推理的依据)