题目内容
矩形的两条对角线夹角为60°，一条较短边的长与一条对角线的长和为15cm，则对角线的长为________cm．
10
分析：要求AC，则必须先求CD．由∠DOC=60°和矩形的性质可知△OCD为等边三角形，从而得到CD=OC=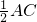
，根据CD+AC=15cm列方程求解．
解答：
解：如图，矩形ABCD中，∠DOC=60°，CD+AC=15cm，求AC
∵∠DOC=60°
∵矩形ABCD
∴OC=OD
∴∠ODC=∠OCD
∴△OCD为等边三角形
∴CD=OC=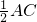
∵CD+AC=15cm
∴
=15cm
∴AC=10cm．
故答案为10．
点评：根据矩形的性质和等边三角形的性质求解．
分析：要求AC，则必须先求CD．由∠DOC=60°和矩形的性质可知△OCD为等边三角形，从而得到CD=OC=
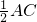，根据CD+AC=15cm列方程求解．解答：
解：如图，矩形ABCD中，∠DOC=60°，CD+AC=15cm，求AC∵∠DOC=60°
∵矩形ABCD
∴OC=OD
∴∠ODC=∠OCD
∴△OCD为等边三角形
∴CD=OC=
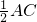
∵CD+AC=15cm
∴
=15cm∴AC=10cm．
故答案为10．
点评：根据矩形的性质和等边三角形的性质求解．
练习册系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
已知一个矩形的两条对角线夹角为60°，一条对角线的长为10cm，则该矩形的周长为（ ）
| A、20cm | ||
B、20
| ||
C、20(1+
| ||
D、10(1+
|
矩形的两条对角线夹角为120°，矩形的宽为3，则矩形的面积是（ ）
A、
| ||
B、3
| ||
C、6
| ||
D、9
|