题目内容
18.用长度一定的绳子围成一个矩形,如果矩形的一边长x(m)与面积y(m2)满足函数关系式y=-x2+24x(0<x<24),则当矩形面积最大时,矩形的一条对角线长为12$\sqrt{2}$m.分析 根据二次函数性质求出面积最大时矩形的一边长及此时矩形的面积,从而得出另一边长,最后由勾股定理可得对角线长度.
解答 解:∵y=-x2+24x=-(x-12)2+144,
∴当x=12时,矩形的面积最大,最大面积为144m2,
则矩形的另一边长为144÷12=12m,
∴对角线长为$\sqrt{1{2}^{2}+1{2}^{2}}$=12$\sqrt{2}$m,
故答案为:12$\sqrt{2}$m.
点评 本题主要考查二次函数的应用及勾股定理,掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
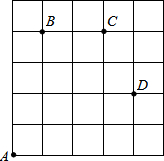 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中 利用如图的两个转盘进行“配紫色”的游戏,用列表法或画树状图求出配得紫色的概率.
利用如图的两个转盘进行“配紫色”的游戏,用列表法或画树状图求出配得紫色的概率. 如右图,以数轴的单位长的线段为边作三个竖立的正方形,以数轴的原点为圆心,OP的长为半径画弧,交数轴于点A,则点A表示的数是-$\sqrt{10}$.
如右图,以数轴的单位长的线段为边作三个竖立的正方形,以数轴的原点为圆心,OP的长为半径画弧,交数轴于点A,则点A表示的数是-$\sqrt{10}$. 在△ABC中,E、F两点都在最长边BC上,BE=BA、CF=CA,又DE∥AB,DF∥AC,求证:△ABF、△ACE、△DEF的外接圆交于一点.
在△ABC中,E、F两点都在最长边BC上,BE=BA、CF=CA,又DE∥AB,DF∥AC,求证:△ABF、△ACE、△DEF的外接圆交于一点.