题目内容
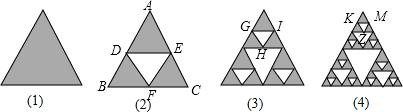
如图(1)是面积为1的阴影三角形,连接它的各边中点.挖去中间的三角形得到图(2).再分别连接剩下的每个阴影三角形的各点中点.挖去中间的三角形得到图(3).再用同样的方法得到图(4).则图(4)中阴影部分的面积为

- A.

- B.

- C.

- D.

D
分析:根据三角形的中位线得出DE∥BC,DE= BC,推出△ADE∽△ABC,
BC,推出△ADE∽△ABC, =
= ,求出△DEF∽△ACB,推出△DEF和△ACB的面积比是(
,求出△DEF∽△ACB,推出△DEF和△ACB的面积比是( )2=
)2= ,求出△DEF的面积,同理求出△GHI和△KZM的面积,根据图形求出即可.
,求出△DEF的面积,同理求出△GHI和△KZM的面积,根据图形求出即可.
解答:∵D是AB中点,E为AC中点,
∴DE∥BC,DE= BC,
BC,
∴△ADE∽△ABC, =
= ,
,
∴ =(
=( )2=
)2= ,
,
∵D是AB中点,E为AC中点,F为BC中点,
∴DE= BC,EF=
BC,EF= AB,DF=
AB,DF= AC,
AC,
∴ =
= =
=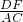 =
= ,
,
∴△DEF∽△ACB,
∴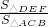 =(
=( )2=
)2= ,
,
∵△ABC的面积是1,
∴△DEF的面积是 ,
,
∴S△DEF=S△ADE,
∴S△DEF=S△ADE= S△ABC=
S△ABC= ,
,
同理求出△GHI和△DEF的面积比是1:4,即 =
= ,
,
∴△GHI的面积是 ×
× =
= ,
,
同理求出△KMZ和△GHI的面积比是1:4,即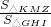 =
= ,
,
∴△KMZ的面积是 ×
× =
=
∴阴影部分的面积是1- -3×
-3× -9×
-9× =
= .
.
故选D.
点评:本题考查了相似三角形的性质和判定,三角形的面积,三角形的中位线等知识点,注意:相似三角形的面积比等于相似比的平方,三角形的中位线平行于第三边,并且等于第三边的一半.
分析:根据三角形的中位线得出DE∥BC,DE=
 BC,推出△ADE∽△ABC,
BC,推出△ADE∽△ABC, =
= ,求出△DEF∽△ACB,推出△DEF和△ACB的面积比是(
,求出△DEF∽△ACB,推出△DEF和△ACB的面积比是( )2=
)2= ,求出△DEF的面积,同理求出△GHI和△KZM的面积,根据图形求出即可.
,求出△DEF的面积,同理求出△GHI和△KZM的面积,根据图形求出即可.解答:∵D是AB中点,E为AC中点,
∴DE∥BC,DE=
 BC,
BC,∴△ADE∽△ABC,
 =
= ,
,∴
 =(
=( )2=
)2= ,
,
∵D是AB中点,E为AC中点,F为BC中点,
∴DE=
 BC,EF=
BC,EF= AB,DF=
AB,DF= AC,
AC,∴
 =
= =
=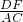 =
= ,
,∴△DEF∽△ACB,
∴
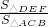 =(
=( )2=
)2= ,
,∵△ABC的面积是1,
∴△DEF的面积是
 ,
,∴S△DEF=S△ADE,
∴S△DEF=S△ADE=
 S△ABC=
S△ABC= ,
,同理求出△GHI和△DEF的面积比是1:4,即
 =
= ,
,∴△GHI的面积是
 ×
× =
= ,
,同理求出△KMZ和△GHI的面积比是1:4,即
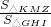 =
= ,
,∴△KMZ的面积是
 ×
× =
=
∴阴影部分的面积是1-
 -3×
-3× -9×
-9× =
= .
.故选D.
点评:本题考查了相似三角形的性质和判定,三角形的面积,三角形的中位线等知识点,注意:相似三角形的面积比等于相似比的平方,三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
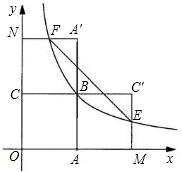 如图,四边形OABC是面积为4的正方形,函数
如图,四边形OABC是面积为4的正方形,函数 (2013•本溪)如图,点B1是面积为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OB1A1的两条中线的交点,再以OB2为一边,构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止.则构造出的最后一个三角形的面积是
(2013•本溪)如图,点B1是面积为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OB1A1的两条中线的交点,再以OB2为一边,构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止.则构造出的最后一个三角形的面积是 (2012•吴中区一模)如图,四边形OABC是面积为4的正方形,函数y=
(2012•吴中区一模)如图,四边形OABC是面积为4的正方形,函数y= (2011•路南区一模)如图,四边形OABC是面积为4的正方形,函数
(2011•路南区一模)如图,四边形OABC是面积为4的正方形,函数