题目内容
8.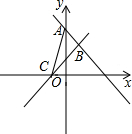 如图,直线y=-$\frac{4}{3}$x+4与y轴交于点A,与直线y=$\frac{4}{5}$x+$\frac{4}{5}$交于点B,且直线y=$\frac{4}{5}$x+$\frac{4}{5}$与x轴交于点C.
如图,直线y=-$\frac{4}{3}$x+4与y轴交于点A,与直线y=$\frac{4}{5}$x+$\frac{4}{5}$交于点B,且直线y=$\frac{4}{5}$x+$\frac{4}{5}$与x轴交于点C.(1)求A、B、C三点坐标;
(2)求△ABC的面积.
分析 (1)根据直线y=-$\frac{4}{3}$x+4与y轴交于点A,与直线y=$\frac{4}{5}$x+$\frac{4}{5}$交于点B,且直线y=$\frac{4}{5}$x+$\frac{4}{5}$与x轴交于点C,可以求得A、B、C三点坐标;
(2)根据A、B、C、D四点坐标和△ABC的面积等于△ACD的面积减去△BCD的面积,可以求得△ABC的面积.
解答 解:(1)如下图所示:直线y=-$\frac{4}{3}$x+4与y轴交于点A,与x轴交于点D.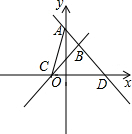
∵直线y=-$\frac{4}{3}$x+4与y轴交于点A,与x轴交于点D,
∴将x=0代入y=-$\frac{4}{3}$x+4,可得,y=4.
将y=0代入y=-$\frac{4}{3}$x+4,可得,x=3.
∴点A的坐标为(0,4),点D的坐标为(3,0).
∵直线y=-$\frac{4}{3}$x+4与直线y=$\frac{4}{5}$x+$\frac{4}{5}$交于点B,
∴$\left\{\begin{array}{l}{y=-\frac{4}{3}x+4}\\{y=\frac{4}{5}x+\frac{4}{5}}\end{array}\right.$.
解得,$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=2}\end{array}\right.$.
∴点B的坐标为($\frac{3}{2},2$).
又∵直线y=$\frac{4}{5}$x+$\frac{4}{5}$与x轴交于点C,
∴将y=0代入y=$\frac{4}{5}$x+$\frac{4}{5}$,可得x=-1.
故点C的坐标为(-1,0).
故点A的坐标为(0,4),点B的坐标为($\frac{3}{2},2$),故点C的坐标为(-1,0).
(2)如下图所示:直线y=-$\frac{4}{3}$x+4与y轴交于点A,与x轴交于点D,作BE⊥CD于点E.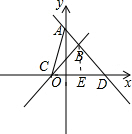
∵点A的坐标为(0,4),点B的坐标为($\frac{3}{2},2$),故点C的坐标为(-1,0),点D的坐标为(3,0),S△ABC=S△ACD-S△BCD.
∴S△ABC=S△ACD-S△BCD=$\frac{CD×OA}{2}-\frac{CD×BE}{2}$=$\frac{4×4}{2}-\frac{4×2}{2}=8-4=4$.
点评 本题考查两条直线相交和求三角形的面积的相关知识,关键是进行灵活变化,将求△ABC的面积转化为求△ACD的面积和△BCD的面积,从而得到△ABC的面积.

 阅读快车系列答案
阅读快车系列答案| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | 无法确定 |
| A. | 8 | B. | -2 | C. | 8或2 | D. | -8或-2 |