题目内容
20. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为( )
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 由旋转的性质得出△ADE≌△ABC,得出∠D=∠B=40°,AE=AC,证出△ACE是等边三角形,得出∠ACE=∠E=60°,由三角形内角和定理求出∠DAE的度数,即可得出结果.
解答 解:由旋转的性质得:△ADE≌△ABC,
∴∠D=∠B=40°,AE=AC,
∵∠CAE=60°,
∴△ACE是等边三角形,
∴∠ACE=∠E=60°,
∴∠DAE=180°-∠E-∠D=80DU
=$\frac{1}{2}$(180°-∠CAE)=$\frac{1}{2}$(180°-60°)=80°,
∴∠DAC=∠DAE-∠CAE=80°-60°=20°;
故选:B.
点评 本题考查了旋转的性质、等边三角形的判定与性质、三角形内角和定理;熟练掌握旋转的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在正方形ABCD中,将△ABP绕B点顺时针旋转,能与△CBP′重合,若BP=a,则PP′=$\sqrt{2}$a.
如图,在正方形ABCD中,将△ABP绕B点顺时针旋转,能与△CBP′重合,若BP=a,则PP′=$\sqrt{2}$a.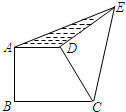 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是1.
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是1.