题目内容
7.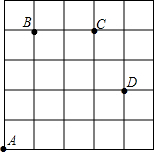 一只甲虫在5×5的方格(每小格边长为1m)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫(A,B,C,D都在格点上).规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
一只甲虫在5×5的方格(每小格边长为1m)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫(A,B,C,D都在格点上).规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中(1)A→C(3,4),B→C(2,0),C→D(+1,-2);
(2)若这只甲虫沿着网格线的行走路线为A→D→C→B,请计算该甲虫走过的最短路程;
(3)若这只甲虫从A处去P处的行走路线依次为(+2,+1),(+3,+2),(-2,-1),(-2,-2),请在图中标出P的位置.
(4)在(3)中甲虫若每走1m需消耗1.5焦耳的能量,则甲虫从A走到P的过程中共需消耗多少焦耳的能量?
分析 (1)根据规定:第一个数表示左右方向,第二个数表示上下方向,结合图形解答;
(2)根据网格图形列式计算即可得解;
(3)根据点的坐标的规定在图形中找出所到达的位置即可得解;
(4)先根据路线求出所走过的路程,然后乘以1.5计算即可得解.
解答 解:(1)A→C(3,4),B→C(2,0),C→D(+1,-2). 故答案为3,4,2,0,D,-2;
故答案为3,4,2,0,D,-2;
(2)(4+2)+(1+2)+2=6+3+2=11;
(3)如图,P在A往右1个单位的格点上;
(4)(2+1)+(3+2)+(2+1)+(2+2)=3+5+3+4=15,
15×1.5=22.5焦耳.
点评 本题考查了坐标确定位置,主要利用了在网格结构找出点的位置的方法,读懂题目信息,理解点的坐标的规定是解题的关键.

练习册系列答案
相关题目
17.下列说法不正确的是( )
| A. | 多项式5x2+4x-2的项是5x2,4x,-2 | B. | 多项式x2-2x+3是二次三项式 | ||
| C. | 2×3,$\frac{a+b}{3}$,$\frac{ab}{2}$,$\frac{3a}{π}$都是单项式 | D. | 3-4a中,一次项的系数是-4 |
2.已知x=2是关于x的方程a(x+1)=$\frac{1}{2}$a+x的解,则a的值是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 已知关于x的多项式(a+5)x|a|-3+3x-3是二次三项式,一次项系数为b,常数项为c,且a、b、c分别是点A、B、C在数轴上对应的数.
已知关于x的多项式(a+5)x|a|-3+3x-3是二次三项式,一次项系数为b,常数项为c,且a、b、c分别是点A、B、C在数轴上对应的数.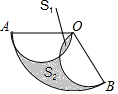 如图,扇形OAB中,OA=OB=2,∠AOB=120°,分别以OA,OB为直径画半圆,若图中两个阴影部分面积分别记为S1与S2,则S2-S1的值是$\frac{1}{3}$π.
如图,扇形OAB中,OA=OB=2,∠AOB=120°,分别以OA,OB为直径画半圆,若图中两个阴影部分面积分别记为S1与S2,则S2-S1的值是$\frac{1}{3}$π.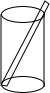 一种盛饮料的圆柱形杯(如图),测得内部底面直径为5cm,高为12cm,吸管放进杯里,杯口外面露出5cm.问吸管要做多长?
一种盛饮料的圆柱形杯(如图),测得内部底面直径为5cm,高为12cm,吸管放进杯里,杯口外面露出5cm.问吸管要做多长?