题目内容
5.AB切⊙O于点A,弦AC=$\sqrt{2}$,∠CAB=45°,则⊙O的直径为( )| A. | 1 | B. | 2 | C. | 4$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 连接AO并延长交⊙O于点D,连接CD,根据条件可证∠ACD=90°,CD=AC=$\sqrt{2}$,由勾股定理即可求得直径.
解答  解:连接AO并延长交⊙O于点D,连接CD,
解:连接AO并延长交⊙O于点D,连接CD,
∵AD是直径,
∴∠ACD=90°,
∵∠CAB=∠CDA=45°,
∴CD=AC=$\sqrt{2}$,
∴AD=$\sqrt{C{D}^{2}+A{C}^{2}}$=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2,
故选B.
点评 本题考查的是切线的性质、圆周角定理及等腰直角三角形的性质,作出辅助线构建直角三角形是解题的关键.

练习册系列答案
相关题目
12.式子|x-2|+|x-4|+|x-4|+|x-8|的最小值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
16. 如图,图中三角形的个数为( )
如图,图中三角形的个数为( )
 如图,图中三角形的个数为( )
如图,图中三角形的个数为( )| A. | 6 | B. | 15 | C. | 18 | D. | 21 |
20.下列分式约分正确的是( )
| A. | $\frac{{a}^{6}}{{a}^{3}}$=a2 | B. | $\frac{x+y}{x-y}$=1 | C. | $\frac{2a{b}^{2}}{6{a}^{2}b}$=$\frac{1}{3}$ | D. | $\frac{m+n}{{m}^{2}+mn}$=$\frac{1}{m}$ |
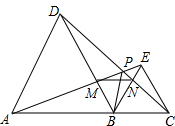 如图,A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接CD、AE交于点P,并分别交BE、BD于N、M,连接MN,下列结论中:①AE=CD;②AM=DP;③MN∥AC; ④若AB=2BC,连接DE,则DE⊥BE;⑤BP平分∠APC.正确的结论有:①③④⑤(填写出所有正确的序号)
如图,A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接CD、AE交于点P,并分别交BE、BD于N、M,连接MN,下列结论中:①AE=CD;②AM=DP;③MN∥AC; ④若AB=2BC,连接DE,则DE⊥BE;⑤BP平分∠APC.正确的结论有:①③④⑤(填写出所有正确的序号)