题目内容
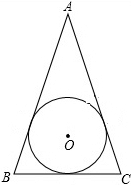 如图,△ABC中,AB=AC=13cm,BC=10cm,⊙O是△ABC的内切圆,求⊙O的半径.
如图,△ABC中,AB=AC=13cm,BC=10cm,⊙O是△ABC的内切圆,求⊙O的半径.考点:三角形的内切圆与内心
专题:
分析:如图,作辅助线;首先求出△ABC的高AD;利用三角形的面积公式列出关于半径r的方程问题即可解决.
解答: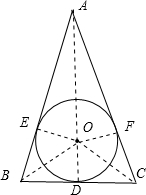 解:如图,连接OA、OB、OC、OD、OE、OF;
解:如图,连接OA、OB、OC、OD、OE、OF;
∵⊙O是△ABC的内切圆,
∴OD⊥BC、OE⊥AB、OF⊥AC;
又∵OE=OF,
∴AO平分∠BAC;而AB=AC,
∴AO⊥BC,
∴AO、OD互相重合,
即AD⊥BC;
∵AB=AC,
∴BD=CD=
BC=5;
由勾股定理得:
AD2=AB2-BD2=132-52=144,
∴AD=12;
设⊙O的半径为r,
则S△ABC=
(AB+AC+BC)r,
S△ABC=
BC•AD,
∴
(13+13+10)r=
×10×12,
解得:r=
,
即⊙O的半径为
.
 解:如图,连接OA、OB、OC、OD、OE、OF;
解:如图,连接OA、OB、OC、OD、OE、OF;∵⊙O是△ABC的内切圆,
∴OD⊥BC、OE⊥AB、OF⊥AC;
又∵OE=OF,
∴AO平分∠BAC;而AB=AC,
∴AO⊥BC,
∴AO、OD互相重合,
即AD⊥BC;
∵AB=AC,
∴BD=CD=
| 1 |
| 2 |
由勾股定理得:
AD2=AB2-BD2=132-52=144,
∴AD=12;
设⊙O的半径为r,
则S△ABC=
| 1 |
| 2 |
S△ABC=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得:r=
| 10 |
| 3 |
即⊙O的半径为
| 10 |
| 3 |
点评:该命题主要考查了三角形的内切圆的性质及其应用问题;解题的关键是首先求出底边上的高,然后利用内切圆的性质,借助三角形的面积公式列出关于半径的方程求解即可.

练习册系列答案
相关题目
在-3.5,
,0,
,0.161161116…中,有理数有( )个.
| 22 |
| 7 |
| π |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
 如图,已知抛物线y=x2+bx+c与x轴交于A、B两点,交y轴负半轴于C点,若∠ACB=90°,且
如图,已知抛物线y=x2+bx+c与x轴交于A、B两点,交y轴负半轴于C点,若∠ACB=90°,且 如图,在Rt△ABC中,AB=AC,点D为BC的中点,∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:①(BE+CF)=
如图,在Rt△ABC中,AB=AC,点D为BC的中点,∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:①(BE+CF)= (1)数轴上表示下列有理数:-1,1
(1)数轴上表示下列有理数:-1,1 已知:如图,点E,F在BC上,BF=CE,∠A=∠D,∠B=∠C,AF与DE交于点O.试说明:
已知:如图,点E,F在BC上,BF=CE,∠A=∠D,∠B=∠C,AF与DE交于点O.试说明: