题目内容
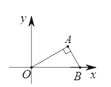
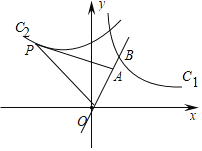
【题目】如图,将曲线c1:y=![]() (x>0)绕原点O逆时针旋转60°得到曲线c2,A为直线y=
(x>0)绕原点O逆时针旋转60°得到曲线c2,A为直线y=![]() x上一点,P为曲线c2上一点,PA=PO,且△PAO的面积为6
x上一点,P为曲线c2上一点,PA=PO,且△PAO的面积为6![]() ,直线y=
,直线y=![]() x交曲线c1于点B,则OB的长( )
x交曲线c1于点B,则OB的长( )
A.2![]() B.5C.3
B.5C.3![]() D.
D.![]()
【答案】A
【解析】
将双曲线逆时针旋转使得l与y轴重合,等腰三角形△PAO的底边在y轴上,应用反比例函数比例系数k的性质解答问题.
如图,将C2及直线y=x绕点O逆时针旋转30°,则得到双曲线C3,直线l与y轴重合.
∴双曲线C3的解析式为y=![]() ,
,
过点P作PM⊥y轴于点M

∵PA=PO
∴M为OA中点.
∵△POA的面积是![]() ,
,
∴S△PAM=S△POM,
∴S△POM=![]() ,
,
∴∴双曲线C3的解析式为y=![]() ,
,
∴双曲线C1的解析式为y=![]() ,
,
由方程组 可得B
可得B![]() ,
,
∴OB=![]() .
.
故选A.

练习册系列答案
相关题目