题目内容
选择合适的方法解下列方程:
(1)4(x+3)2=25;
(2)3x(x+2)=4(x-1)+7.
(1)4(x+3)2=25;
(2)3x(x+2)=4(x-1)+7.
考点:解一元二次方程-公式法,解一元二次方程-直接开平方法
专题:计算题
分析:(1)方程变形后,利用平方根定义开方即可求出解;
(2)方程整理后找出a,b,c的值,计算出根的判别式的值大于0,代入求根公式即可求出解.
(2)方程整理后找出a,b,c的值,计算出根的判别式的值大于0,代入求根公式即可求出解.
解答:解:(1)方程变形得:(x+3)2=
,
开方得:x+3=±
,
解得:x1=-
,x2=-
;
(2)方程整理得:3x2+2x-3=0,
这里a=3,b=2,c=-3,
∵△=4+36=40,
∴x=
=
.
| 25 |
| 4 |
开方得:x+3=±
| 5 |
| 2 |
解得:x1=-
| 1 |
| 2 |
| 11 |
| 2 |
(2)方程整理得:3x2+2x-3=0,
这里a=3,b=2,c=-3,
∵△=4+36=40,
∴x=
-2±2
| ||
| 6 |
-1±
| ||
| 3 |
点评:此题考查了解一元二次方程-公式法与直接开方法,熟练掌握各自解法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列计算正确的是( )
| A、a3+a2=2a5 |
| B、(2a3)2=4a6 |
| C、(a+b)2=a2+b2 |
| D、a6÷a2=a3 |
 如图,直线AB、CD相交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,求∠AOE和∠DOF的度数.
如图,直线AB、CD相交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,求∠AOE和∠DOF的度数.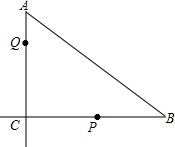 如图,在Rt△ABC中,∠BCA=90°,AC=6cm,BC=8cm.有一动点P从B点出发,在射线BC方向移动,速度是2cm/s,在P点出发后2秒后另一个动点Q从A点出发,在射线AC方向移动,速度是1cm/s.若设P出发后时间为t秒.
如图,在Rt△ABC中,∠BCA=90°,AC=6cm,BC=8cm.有一动点P从B点出发,在射线BC方向移动,速度是2cm/s,在P点出发后2秒后另一个动点Q从A点出发,在射线AC方向移动,速度是1cm/s.若设P出发后时间为t秒.
 如图,有一圆锥形粮仓,其轴截面△SAB为正三角形,边长为6m,母线SB的中点P处有一老鼠正偷吃粮食,小猫从A处沿圆锥的表面偷袭老鼠,则小猫经过的最短路程是多少米?
如图,有一圆锥形粮仓,其轴截面△SAB为正三角形,边长为6m,母线SB的中点P处有一老鼠正偷吃粮食,小猫从A处沿圆锥的表面偷袭老鼠,则小猫经过的最短路程是多少米?