题目内容
 我们知道,如果两个锐角的和等于一直角,那么这两个角互为余角,简称互余.如图,∠A与∠B互余,且有:sinA=
我们知道,如果两个锐角的和等于一直角,那么这两个角互为余角,简称互余.如图,∠A与∠B互余,且有:sinA= ,cosB=
,cosB= ,因此知sinA=cosB,注意到在△ABC中,∠A+∠B=90°,即∠B=90°-∠A,∠A=90°-∠B,于是有:sin(90°-A)=cosA,cos(90°-A)=sinA.
,因此知sinA=cosB,注意到在△ABC中,∠A+∠B=90°,即∠B=90°-∠A,∠A=90°-∠B,于是有:sin(90°-A)=cosA,cos(90°-A)=sinA.
试完成下列选择题:
如果α是锐角,且cosα= ,那么sin(90°-α)的值等于
,那么sin(90°-α)的值等于
- A.

- B.

- C.

- D.

B
分析:阅读理解:一个角的正弦值等于它的余角的余弦值.
解答:∵cosα= ,
,
∴sin(90°-α)=cosα= .
.
故选B.
点评:掌握互为余角的正余弦关系:一个角的正弦值等于它的余角的余弦值.
分析:阅读理解:一个角的正弦值等于它的余角的余弦值.
解答:∵cosα=
 ,
,∴sin(90°-α)=cosα=
 .
.故选B.
点评:掌握互为余角的正余弦关系:一个角的正弦值等于它的余角的余弦值.

练习册系列答案
相关题目
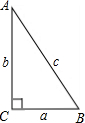 我们知道,如果两个锐角的和等于一直角,那么这两个角互为余角,简称互余.如图,∠A与∠B互余,且有:sinA=
我们知道,如果两个锐角的和等于一直角,那么这两个角互为余角,简称互余.如图,∠A与∠B互余,且有:sinA=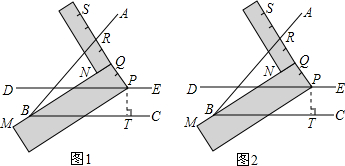 (1)阅读理解:
(1)阅读理解: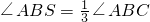 是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出
是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出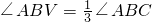 (无需写画法,保留画图痕迹即可).
(无需写画法,保留画图痕迹即可). ,cosB=
,cosB= ,因此知sinA=cosB,注意到在△ABC中,∠A+∠B=90°,即∠B=90°-∠A,∠A=90°-∠B,于是有:sin(90°-A)=cosA,cos(90°-A)=sinA.
,因此知sinA=cosB,注意到在△ABC中,∠A+∠B=90°,即∠B=90°-∠A,∠A=90°-∠B,于是有:sin(90°-A)=cosA,cos(90°-A)=sinA. ,那么sin(90°-α)的值等于( )
,那么sin(90°-α)的值等于( )




 ,cosB=
,cosB= ,因此知sinA=cosB,注意到在△ABC中,∠A+∠B=90°,即∠B=90°﹣∠A,∠A=90°﹣∠B,于是有:sin(90°﹣A)=cosA,cos(90°﹣A)=sinA.试完成下列选择题:如果α是锐角,且cosα=
,因此知sinA=cosB,注意到在△ABC中,∠A+∠B=90°,即∠B=90°﹣∠A,∠A=90°﹣∠B,于是有:sin(90°﹣A)=cosA,cos(90°﹣A)=sinA.试完成下列选择题:如果α是锐角,且cosα= ,那么sin(90°﹣α)的值等于
,那么sin(90°﹣α)的值等于



