��Ŀ����
��ͼ����֪����Rt��ABC����ACB=90�㣬CA=CB����BCΪ���������ȱߡ�CBA������AD������C����ACB�Ľ�ƽ������AD���ڵ�E������BE��
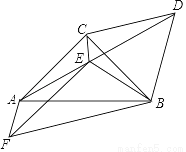
��1����AE=2����CE�ij��ȣ�
��2����ABΪ����������AFB����AFB=60�㣬����FE����֤��FA+FB= 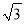 FE��
FE��
��ϰ��ϵ�д�
 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
�����Ŀ


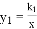 ��һ�κ���
��һ�κ���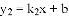 ��ͼ���ڵ�A��1��8����B��-4��m������.
��ͼ���ڵ�A��1��8����B��-4��m������.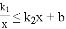 �Ľ⡣
�Ľ⡣ 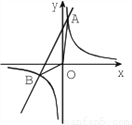
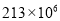 B.
B. 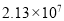 C.
C. 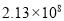 D.
D. 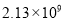
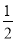 ��
��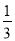 ����
����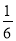 ����
����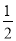 ��(��
��(��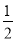 )����1.����������һ�£���һ��������(�� )
)����1.����������һ�£���һ��������(�� )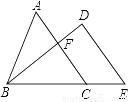
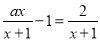 �Ľ�Ϊ���������ҹ���x�IJ���ʽ��
�Ľ�Ϊ���������ҹ���x�IJ���ʽ�� �⣬��ô������������������a�ĺ��ǣ� ��
�⣬��ô������������������a�ĺ��ǣ� ��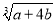 ��ֵ��
��ֵ��