题目内容
作出函数y=4x-1的图象,并根据图象回答下列问题:
(1)y的值随x值的增大怎样变化?
(2)指出图象与x轴交点A、与y轴交点B的坐标,并求出△AOB的面积S.
(3)指出当x为何值时,y>0,y=0,y<0?
(4)若函数y=-x+m2与y=4x-1的图象交于x轴上同一点,求m的值.
(1)y的值随x值的增大怎样变化?
(2)指出图象与x轴交点A、与y轴交点B的坐标,并求出△AOB的面积S.
(3)指出当x为何值时,y>0,y=0,y<0?
(4)若函数y=-x+m2与y=4x-1的图象交于x轴上同一点,求m的值.
分析:(1)根据图象的变化趋势即可确定函数的增减性;
(2)根据图象直接指出交点坐标即可;
(3)当函数图象位于x轴的上方时,y>0从而可以确定自变量的取值范围;
(4)首先求得函数y=4x-1与x轴的交点,然后将交点坐标代入函数y=-x+m2,即可求得m的值.
(2)根据图象直接指出交点坐标即可;
(3)当函数图象位于x轴的上方时,y>0从而可以确定自变量的取值范围;
(4)首先求得函数y=4x-1与x轴的交点,然后将交点坐标代入函数y=-x+m2,即可求得m的值.
解答:解:∵令x=0得y=-1,令y=0得4x-1=0,求得x=
.
∴图象为:

(1)观察图象知y随x的增大而增大;
(2)图象与x轴交与点A(
,0),与y轴交与点B(0,-1),
故△AOB的面积S=
×
×1=
;
(3)当x>
时,y>0,
当x=
时,y=0,
当x<
时,y<0;
(4)∵将点A的坐标代入y=-x+m2,得0=-
+m2,
∴m=±
.
| 1 |
| 4 |
∴图象为:

(1)观察图象知y随x的增大而增大;
(2)图象与x轴交与点A(
| 1 |
| 4 |
故△AOB的面积S=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
(3)当x>
| 1 |
| 4 |
当x=
| 1 |
| 4 |
当x<
| 1 |
| 4 |
(4)∵将点A的坐标代入y=-x+m2,得0=-
| 1 |
| 4 |
∴m=±
| 1 |
| 2 |
点评:本题考查了一次函数的图象,解题的关键是利用两点法作出函数的图象,然后确定各题的答案.

练习册系列答案
相关题目

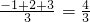 ,min{-1,2,3}=-1,min{-1,2,a}=
,min{-1,2,3}=-1,min{-1,2,a}=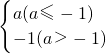

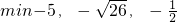 =______;
=______;