题目内容
9. 如图,平行四边形ABCD的对角线AC、BD交于点O,EF过点O且与AD、BC交于点E、F.求证:OE=OF.
如图,平行四边形ABCD的对角线AC、BD交于点O,EF过点O且与AD、BC交于点E、F.求证:OE=OF.
分析 由平行四边形ABCD,可得AD∥BC,OA=OC,即可证得∠EAO=∠FCO,继而利用ASA证得△AOE≌△COF,即可证得OE=OF.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{OA=OC}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴OE=OF.
点评 此题考查了平行四边形的性质以及全等三角形的判定与性质.注意证得△AOE≌△COF是关键.

练习册系列答案
相关题目
4.不等式3x-1>x+3的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
19.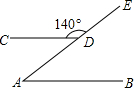 如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )
如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )
 如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )
如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )| A. | 140° | B. | 60° | C. | 50° | D. | 40° |
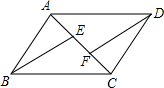 已知平行四边形ABCD中,BE∥DF,求证:AE=CF.
已知平行四边形ABCD中,BE∥DF,求证:AE=CF. 如图,在△ABC中,AD是边BC上的中线,设向量$\overline{AB}$=$\overline{a}$,$\overline{AD}$=$\overline{b}$,如果用向量$\overline{a}$,$\overline{b}$表示向量$\overline{BC}$,那$\overline{BC}$=2$\overline{b}$-2$\overline{a}$.
如图,在△ABC中,AD是边BC上的中线,设向量$\overline{AB}$=$\overline{a}$,$\overline{AD}$=$\overline{b}$,如果用向量$\overline{a}$,$\overline{b}$表示向量$\overline{BC}$,那$\overline{BC}$=2$\overline{b}$-2$\overline{a}$.