题目内容
如图,E,F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE、BF交于点P
(1)求证:CE=BF;
(2)求∠BPC的度数.

(1)证明:如图,∵△ABC是等边三角形,
∴BC=AB,∠A=∠EBC=60°,
∴在△BCE与△ABF中,
 ,
,
∴△BCE≌△ABF(SAS),
∴CE=BF;
(2)∵由(1)知△BCE≌△ABF,
∴∠BCE=∠ABF,
∴∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°,即∠PBC+∠PCB=60°,
∴∠BPC=180°﹣60°=120°.
即:∠BPC=120°.


练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
某小区为了排污,需铺设一段全长为720米的排污管道,为减少施工对居民生活的影响,须缩短施工时间,实际施工时每天的工作效率比原计划提高20%,结果提前2天完成任务.设原计划每天铺设x米,下面所列方程正确的是( )
|
| A. |
| B. |
|
|
| C. |
| D. |
|
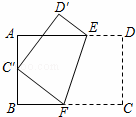
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
|
| A. | 4 | B. | 3 | C. | 4.5 | D. | 5 |
 ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1,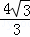 ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.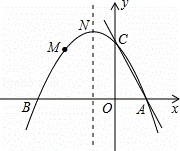
 ﹣
﹣ =2
=2 ﹣
﹣ =
=
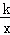 (k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.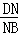 的值.
的值.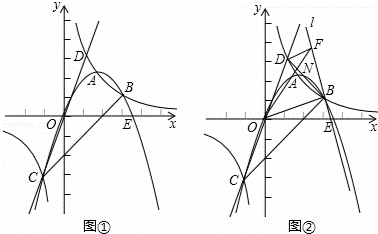

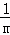 +
+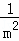 +
+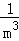 +…+
+…+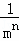 (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).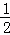 +
+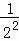 +
+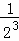 +…+
+…+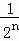 .
.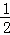 ;
;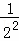 ;
;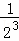 +…+
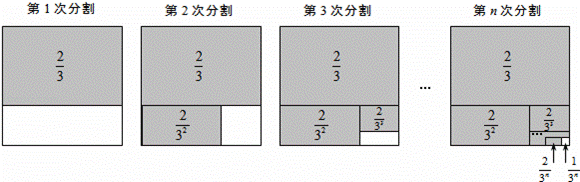
+…+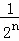 ,最后空白部分的面积是
,最后空白部分的面积是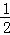 +
+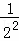 +
+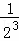 +…+
+…+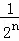 =1﹣
=1﹣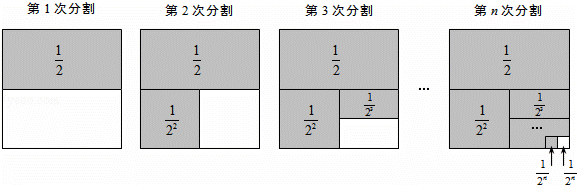
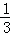 +
+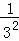 +
+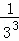 +…+
+…+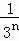 .
.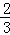 ;
;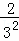 ;
;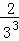 +…+
+…+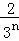 ,最后空白部分的面积是
,最后空白部分的面积是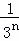 .
.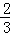 +
+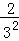 +
+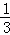 +
+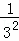 +
+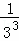 +…+
+…+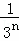 =
=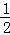 ﹣
﹣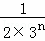 .
.
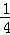 +
+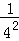 +
+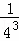 +…+
+…+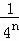 .
.
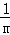 +
+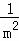 +
+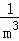 +…+
+…+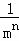 .
.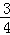 +
+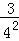 +
+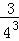 +…+
+…+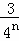 =1﹣
=1﹣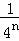 ,
,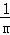 +
+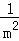 +
+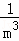 +…+
+…+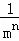 =
= 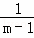 ﹣
﹣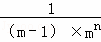 .
.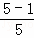 +
+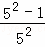 +
+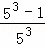 +…+
+…+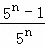 .
. (k>0)的图象上,则y1 y2(填“>”“<”或“=”)
(k>0)的图象上,则y1 y2(填“>”“<”或“=”)