��Ŀ����
��ѧ���⣺����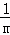 +
+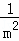 +
+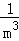 +��+
+��+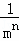 ������m��n��������������m��2��n��1����
������m��n��������������m��2��n��1����
̽�����⣺Ϊ����������ѧ���⣬�����������ν�ϵ�˼�뷽����ͨ�����ϵطָ�һ�����Ϊ1�������Σ���������ϵ�ͼ���ͼ������ؽ������������ȡһ���������⻯�IJ���������̽����
̽��һ������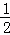 +
+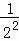 +
+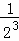 +��+
+��+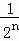 ��
��
��1�ηָ�������ε�������ȷ֣�������Ӱ���ֵ����Ϊ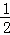 ��
��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣���Ӱ���ֵ����֮��Ϊ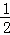 +
+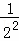 ��
��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ȷ֣�������Ӱ���ֵ����֮��Ϊ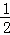 +
+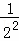 +
+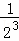 +��+
+��+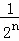 �����հײ��ֵ������
�����հײ��ֵ������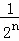 ��
��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��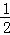 +
+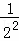 +
+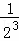 +��+
+��+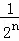 =1��
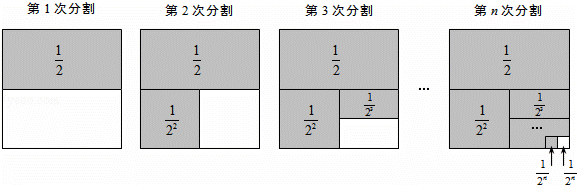
=1��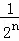 ��
��
̽����������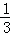 +
+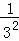 +
+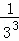 +��+
+��+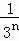 ��
��
��1�ηָ�������ε�������ȷ֣�������Ӱ���ֵ����Ϊ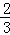 ��
��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣���Ӱ���ֵ����֮��Ϊ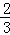 +
+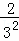 ��
��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ����������ȷ֣�������Ӱ���ֵ����֮��Ϊ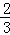 +
+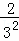 +
+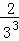 +��+
+��+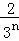 �����հײ��ֵ������
�����հײ��ֵ������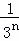 ��
��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��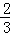 +
+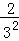 +
+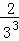 +��+
+��+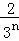 =1��
=1��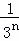 ��
��
����ͬ����2����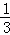 +
+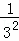 +
+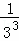 +��+
+��+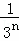 =
=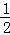 ��
��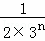 ��
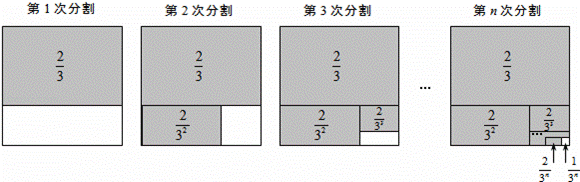
��
̽����������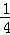 +
+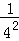 +
+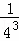 +��+
+��+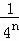 ��
��
����������������ֻ������n�ηָ�ͼ����ͼ�ϱ�ע��Ӱ�����������д��̽�����̣�

������⣺����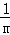 +
+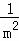 +
+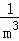 +��+
+��+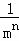 ��
��
��ֻ�軭����n�ηָ�ͼ����ͼ�ϱ�ע��Ӱ��������������������գ�
���ݵ�n�ηָ�ͼ�ɵõ�ʽ����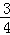 +
+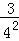 +
+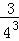 +��+
+��+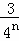 =1��
=1��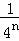 ����
����
���ԣ�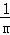 +
+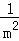 +
+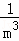 +��+
+��+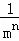 =��
=��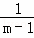 ��
��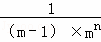 ����
����
�ع�Ӧ�ã����� 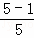 +
+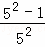 +
+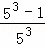 +��+
+��+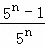 ��
��
�⣺̽��������1�ηָ�������ε�����ĵȷ֣�

������Ӱ���ֵ����Ϊ ��
��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ĵȷ֣�
��Ӱ���ֵ����֮��Ϊ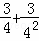 ��
��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ĵȷ֣�
����
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ��������ĵȷ֣�
������Ӱ���ֵ����֮��Ϊ�� +
+ +
+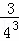 +��+
+��+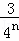 ��
��
���Ŀհײ��ֵ������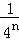 ��
��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ�� +
+ +
+ +��+
+��+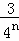 =1��
=1�� ��
��
����ͬ����3���� +
+ +
+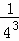 +��+
+��+ =
=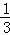 ��
��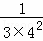 ��
��
������⣺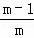 +
+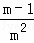 +
+ +��+
+��+ =1��
=1��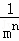 ��
��
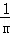 +
+ +
+ +��+
+��+ =
=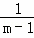 ��
��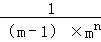 ��
��
�ʴ�Ϊ�� +
+ +
+ +��+
+��+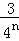 =1��
=1��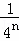 ��
��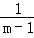 ��
�� ��
��

�ع�Ӧ�ã� +
+ +
+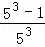 +��+
+��+ ��
��
=1��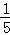 +1��
+1��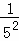 +1��
+1��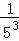 +��+1��
+��+1�� ��
��
=n����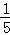 +
+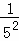 +
+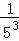 +��+
+��+ ����
����
=n���� ��
�� ����
����
=n�� +
+ ��
��

 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�ij�����12����Ա�����������
| ���䣨�꣩ | 18 | 19 | 20 | 21 |
| ���� | 5 | 4 | 1 | 2 |
����12����Ա�����������ƽ�����ֱ��ǣ�������
| �� | A�� | 18��19 | B�� | 19��19 | C�� | 18��19.5 | D�� | 19��19.5 |
��ͳ���ҹ�2014��ǰ�����ѿ�������286���ױ��Ϸ�������286���ÿ�ѧ��������ʾΪ��������
| �� | A�� | 2.86��106 | B�� | 2.86��107 | C�� | 28.6��105 | D�� | 0.286��107 |


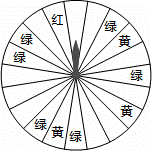
 +��
+�� ��2014��0��2cos30�㩁��
��2014��0��2cos30�㩁�� ����1��
����1��