题目内容
 如图,以Rt△ABC(∠ACB=90°)的三边为边长分别向外作正方形ABDE、BCGF、ACHM,连接DF、EM、GH.已知AB=5,BC=3,求六边形DEMHGF的面积.
如图,以Rt△ABC(∠ACB=90°)的三边为边长分别向外作正方形ABDE、BCGF、ACHM,连接DF、EM、GH.已知AB=5,BC=3,求六边形DEMHGF的面积.考点:全等三角形的判定与性质,勾股定理
专题:
分析:易证sin∠DBF=sin∠ABC,即可求得S△DBF=S△ACB,同理可得S△AEM=S△CGH=S△ACB,根据六边形DEMHGF的面积=正方形ABDE面积+正方形BCGF面积+正方形ACHM面积+4S△ACB即可解题.
解答:解:∵∠ABD+∠CBF=90°+90°=180°,
∴∠DBF+∠ABC=180°,
∴sin∠DBF=sin∠ABC,
∵S△DBF=
BD•BF•sin∠DBF,S△ACB=
AB•BC•sin∠ABC,
∴S△DBF=S△ACB,
同理S△AEM=S△CGH=S△ACB,
∴六边形DEMHGF的面积=正方形ABDE面积+正方形BCGF面积+正方形ACHM面积+4S△ACB,
∵AB=5,BC=3,
∴AC=
=4,
∴六边形DEMHGF的面积=52+42+32+
×3×4=56.
∴∠DBF+∠ABC=180°,
∴sin∠DBF=sin∠ABC,
∵S△DBF=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△DBF=S△ACB,
同理S△AEM=S△CGH=S△ACB,
∴六边形DEMHGF的面积=正方形ABDE面积+正方形BCGF面积+正方形ACHM面积+4S△ACB,
∵AB=5,BC=3,
∴AC=
| AB2-BC2 |
∴六边形DEMHGF的面积=52+42+32+
| 1 |
| 2 |
点评:此题考查了三角形面积的计算,考查了直角三角形中勾股定理的运用,本题中求证S△DBF=S△AEM=S△CGH=S△ACB是解题的关键.

练习册系列答案
相关题目
 如图所示,一立体图形圆台,它的俯视图是右面的四幅图中的( )
如图所示,一立体图形圆台,它的俯视图是右面的四幅图中的( )A、 |
B、 |
C、 |
D、 |
把分式方程
-
=1去分母后所得结果正确的是( )
| 1 |
| x-2 |
| 1-x |
| 2-x |
| A、1-(1-x)=1 |
| B、1+(1-x)=1 |
| C、1-(1-x)=x-2 |
| D、1+(1-x)=x-2 |
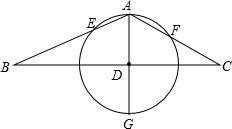 如图,由△ABC的顶点A作高AD,以垂足D为圆心,AD为半径作圆,分别交AB、AC于EF,若AE=2,AF=3,AB=5,求AC的长.
如图,由△ABC的顶点A作高AD,以垂足D为圆心,AD为半径作圆,分别交AB、AC于EF,若AE=2,AF=3,AB=5,求AC的长.