题目内容
线段y=-| 1 | 2 |
分析:根据k相等得到AD∥BC,根据A与B的横坐标都是1,D与C的横坐标都是3得到AB∥CD,根据平行四边形的面积公式求出即可.
解答: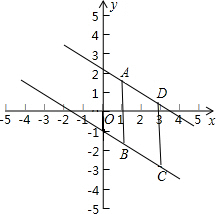 解:当a=-1时,y=-
解:当a=-1时,y=-
x-1,
当a=2时,y=-
x+2,
∵k=-
,
∴AD∥BC,
当x=1时,y=-
x-1=-
,
∴B的坐标是(1,-
),
同法可求A得坐标是(1,
),C的坐标是(3,-
),D的坐标是(3,
),
∴AB∥CD,
∴平行四边形ABCD的面积是AB×(3-1)=(
+
)×2=6,
故答案为:6.
 解:当a=-1时,y=-
解:当a=-1时,y=-| 1 |
| 2 |
当a=2时,y=-
| 1 |
| 2 |
∵k=-
| 1 |
| 2 |
∴AD∥BC,
当x=1时,y=-
| 1 |
| 2 |
| 3 |
| 2 |
∴B的坐标是(1,-
| 3 |
| 2 |
同法可求A得坐标是(1,
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
∴AB∥CD,
∴平行四边形ABCD的面积是AB×(3-1)=(
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:6.
点评:本题主要考查对平行四边形的性质,一次函数图象上点的坐标特征,一次函数的性质等知识点的理解和掌握,能推出四边形是平行四边形是解此题的关键.

练习册系列答案
相关题目
线段y=-
x+a(1≤x≤3),当a的值由-1增加到2时,该线段运动所经过的平面区域的面积为( )
| 1 |
| 2 |
| A、6 | B、8 | C、9 | D、10 |
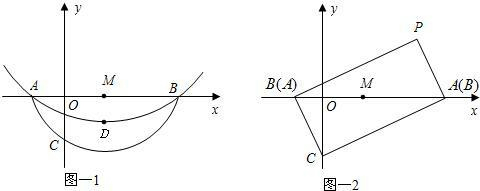
 在平面直角坐标系内,点O为坐标原点,直线y=
在平面直角坐标系内,点O为坐标原点,直线y= 如图,直线y=-x+1与x轴、y轴分别交于A、B两点,P(a,b)是反比例函数y=
如图,直线y=-x+1与x轴、y轴分别交于A、B两点,P(a,b)是反比例函数y=