题目内容
线段y=-
x+a(1≤x≤3),当a的值由-1增加到2时,该线段运动所经过的平面区域的面积为( )
| 1 |
| 2 |
| A、6 | B、8 | C、9 | D、10 |
分析:根据a的值由-1增加到2,且1≤x≤3,分别将端点代入解析式,可以得出四个关键点,根据图象可以判断出它的形状,从而求出图形的面积.
解答: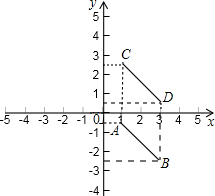 解:根据1≤x≤3,a的值由-1增加到2,
解:根据1≤x≤3,a的值由-1增加到2,
∴当a=-1,x=1时,y=-
,x=3时,y=-
,
当a=2,x=1时,y=
,x=3时,y=
,
在坐标系中找出各点,作出图形,可知:
运动经过的平面区域是个平行四边形的区域,
高是x的变化值3-1=2,底是y的变化值2-(-1)=3,
则所求面积=(3-1)×[2-(-1)]=6.
故选:A.
 解:根据1≤x≤3,a的值由-1增加到2,
解:根据1≤x≤3,a的值由-1增加到2,∴当a=-1,x=1时,y=-
| 3 |
| 2 |
| 5 |
| 2 |
当a=2,x=1时,y=
| 3 |
| 2 |
| 1 |
| 2 |
在坐标系中找出各点,作出图形,可知:
运动经过的平面区域是个平行四边形的区域,
高是x的变化值3-1=2,底是y的变化值2-(-1)=3,
则所求面积=(3-1)×[2-(-1)]=6.
故选:A.
点评:此题主要考查了一次函数中分段函数的移动问题,以及平行四边形的面积求法等知识,作出关键的线段端点,得出平移前后的图形是解决问题的关键.

练习册系列答案
相关题目
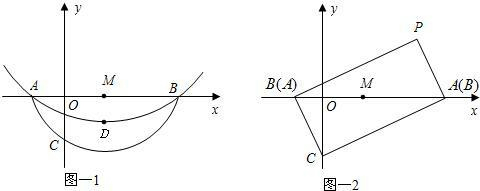
 在平面直角坐标系内,点O为坐标原点,直线y=
在平面直角坐标系内,点O为坐标原点,直线y= 如图,直线y=-x+1与x轴、y轴分别交于A、B两点,P(a,b)是反比例函数y=
如图,直线y=-x+1与x轴、y轴分别交于A、B两点,P(a,b)是反比例函数y=