题目内容
13. 如图,在△ABC中,∠C=90°,CB=6,AB的垂直平分线分别交AB、AC于点D、E,CD=5.
如图,在△ABC中,∠C=90°,CB=6,AB的垂直平分线分别交AB、AC于点D、E,CD=5.(1)求线段AC的长;
(2)求线段AE的长.
分析 (1)根据直角三角形的性质得到AB=2CD=10,根据勾股定理计算即可;
(2)连接BE,设AE=x,根据线段垂直平分线的性质得到BE=AE=x,根据勾股定理列出关于x的方程,解方程即可.
解答 解:(1)∵AB的垂直平分线,
∴CD为中线,
∵∠C=90°,
∴AB=2CD=10,
∵∠C=90°,
∴$AC=\sqrt{A{B^2}-B{C^2}}=\sqrt{100-36}=8$;
(2)连接BE,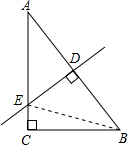
设AE=x,
∵AB的垂直平分线,
∴BE=AE=x,
∴CE=8-x,
∵∠C=90°,
∴CE2+BC2=BE2,
∴(8-x)2+62=x2,
解得:$x=\frac{25}{4}$,
∴线段AE的长为$\frac{25}{4}$.
点评 本题考查的是线段垂直平分线的性质和勾股定理的应用,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
 如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )| A. | 先变小,后变大 | B. | 先变大,后变小 | ||
| C. | DE与OD的长度保持相等 | D. | 固定不变 |
 如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论正确的有( )个.
如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论正确的有( )个. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3)
如图,函数y=2x和y=ax+4的图象相交于点A(m,3)