题目内容
 四边形ABCD是直角梯形,AB∥DC,AD⊥DC,AB=AD=5,∠BCD=45°,求梯形的周长.
四边形ABCD是直角梯形,AB∥DC,AD⊥DC,AB=AD=5,∠BCD=45°,求梯形的周长.
 解:过B作BE∥AD交DC于E,
解:过B作BE∥AD交DC于E,∵AB∥DC,BE∥AD,
∴四边形ADEB是平行四边形,
∴AD=BE=5,
AB=DE=5,
∵AD⊥DC,
∴∠D=∠BEC=90°,
∵∠C=45°,
∴∠EBC=180°-90°-45°=45°,
即:∠EBC=∠C,
∴EC=BE=5,
在△BEC中,由勾股定理得:BC=5
 ,
,∴DC=5+5=10,
∴梯形的周长是AB+BC+AD+DC=20+5
 .
.答:梯形的周长是20+5
 .
.分析:过B作BE∥AD交DC于E,得到□ADEB,求出BE、DE的长度,由∠BCD=45°,推出∠EBC=∠C,根据勾股定理即可求出BC的长,代入即可求出答案.
点评:本题主要考查了平行四边形的性质和判定,三角形的内角和定理,勾股定理,直角梯形等知识点,解此题的关键是作辅助线把直角梯形转化成平行四边形和直角三角形,题型较好,综合性比较强.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
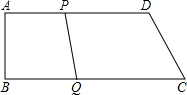
 如图,已知四边形ABCD是直角梯形,AD∥BC,AB⊥BC,四边形ADEF是矩形,其面积为6.28cm2,求阴影部分的面积.
如图,已知四边形ABCD是直角梯形,AD∥BC,AB⊥BC,四边形ADEF是矩形,其面积为6.28cm2,求阴影部分的面积.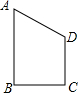 (2013•杭州)四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1,S2,则|S1-S2|=
(2013•杭州)四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1,S2,则|S1-S2|=