题目内容
若一次函数y=kx+3的图象与坐标的两个交点的距离是5,且y随x的增大而减小,则k的值为 .
考点:一次函数的性质
专题:数形结合
分析:先求出一次函数与y轴的交点坐标为(0,3),设一次函数与x轴的交点坐标为(t,0),利用勾股定理得到t2+32=52,解得t=4或t=-4,由于y随x的增大而减小,根据一次函数的性质得t=4,即一次函数与x轴的交点坐标为(4,0),然后把(4,0)代入y=kx+3即可计算出k的值.
解答:解:当x=时,y=kx+3=0,则一次函数与y轴的交点坐标为(0,3),
设一次函数与x轴的交点坐标为(t,0),
因为一次函数y=kx+3的图象与坐标的两个交点的距离是5,
所以t2+32=52,解得t=4或t=-4,
而y随x的增大而减小,
所以t=4,即一次函数与x轴的交点坐标为(4,0),
把(4,0)代入y=kx+3得4k+3=0,解得k=-
.
故答案为-
.
设一次函数与x轴的交点坐标为(t,0),
因为一次函数y=kx+3的图象与坐标的两个交点的距离是5,
所以t2+32=52,解得t=4或t=-4,
而y随x的增大而减小,
所以t=4,即一次函数与x轴的交点坐标为(4,0),
把(4,0)代入y=kx+3得4k+3=0,解得k=-
| 3 |
| 4 |
故答案为-
| 3 |
| 4 |
点评:本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.

练习册系列答案
相关题目
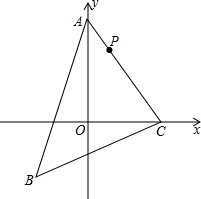 如图,已知△ABC三个顶点坐标分别为A(0,4),B(-2,-2),C(3,0),点P在线段AC上移动.当点P坐标为(1,m)时,请在y轴上找点Q,使△PQC周长最小.
如图,已知△ABC三个顶点坐标分别为A(0,4),B(-2,-2),C(3,0),点P在线段AC上移动.当点P坐标为(1,m)时,请在y轴上找点Q,使△PQC周长最小.