题目内容
 如图,∠MON=90°,矩形ABCD的顶点A,B分别在OM、ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=
如图,∠MON=90°,矩形ABCD的顶点A,B分别在OM、ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=| 3 |
A、
| ||
B、
| ||
| C、2 | ||
D、2-
|
考点:勾股定理,三角形三边关系,直角三角形斜边上的中线
专题:
分析:取AB的中点,连接OE、DE,根据直角三角形斜边上的中线等于斜边的一半求出OE,利用勾股定理列式求出DE,然后根据三角形的任意两边之和大于第三边判断出O、E、D三点共线时点D到点O的距离最大,过点A作AF⊥OD于F,利用∠ADE的余弦列式求出DF,从而得到点F是OD的中点,判断出AF垂直平分OD,再根据线段垂直平分线上的点到两端点的距离相等可得OA=AD.
解答: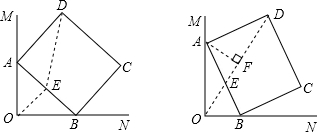 解:如图,取AB的中点,连接OE、DE,
解:如图,取AB的中点,连接OE、DE,
∵∠MON=90°,
∴OE=AE=
AB=
×2=1,
∵三边形ABCD是矩形,
∴AD=BC=
,
在Rt△ADE中,由勾股定理得,DE=
=
=2,
由三角形的三边关系得,O、E、D三点共线时点D到点O的距离最大,
此时,OD=OE+DE=1+2=3,
过点A作AF⊥OD于F,则cos∠ADE=
=
,
即
=
,
解得DF=
,
∵OD=3,
∴点F是OD的中点,
∴AF垂直平分OD,
∴OA=AD=
.
故选B.
 解:如图,取AB的中点,连接OE、DE,
解:如图,取AB的中点,连接OE、DE,∵∠MON=90°,
∴OE=AE=
| 1 |
| 2 |
| 1 |
| 2 |
∵三边形ABCD是矩形,
∴AD=BC=
| 3 |
在Rt△ADE中,由勾股定理得,DE=
| AD2+AE2 |
(
|
由三角形的三边关系得,O、E、D三点共线时点D到点O的距离最大,
此时,OD=OE+DE=1+2=3,
过点A作AF⊥OD于F,则cos∠ADE=
| AD |
| DE |
| DF |
| AD |
即
| ||
| 2 |
| DF | ||
|
解得DF=
| 3 |
| 2 |
∵OD=3,
∴点F是OD的中点,
∴AF垂直平分OD,
∴OA=AD=
| 3 |
故选B.
点评:本题考查了勾股定理,三角形的任意两边之和大于第三边,直角三角形斜边上的中线等于斜边的一半的性质,线段垂直平分线上的点到两端点的距离相等的性质,作辅助线并判断出OD最大时的情况是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
如图,把一个正三角形分成四个全等的三角形,第一次挖去中间一个小三角形,对剩下的三个小三角形再重复以上做法…一直到第六次挖去后剩下的三角形有( )


| A、35 |
| B、35+1 |
| C、36 |
| D、36+1 |
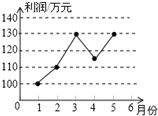 某企业1~5月份利润的变化情况图,以下说法中与图中反映的信息相符的是( )
某企业1~5月份利润的变化情况图,以下说法中与图中反映的信息相符的是( )| A、1~2月份利润的增长快于2~3月份利润的增长 |
| B、1~5月份利润的众数是130万元 |
| C、1~4月份利润的极差与1~5月份利润的极差不同 |
| D、1~5月份利润的中位数为120万元 |
下列运算正确的是( )
| A、x6÷x2=x4 |
| B、(x3)3=x6 |
| C、x3•x2=x6 |
| D、x5+x5=x10 |
一个正方形的面积是13,估计它的边长大小在( )
| A、2与3之间 |
| B、3与4之间 |
| C、4与5之间 |
| D、5与6之间 |
 如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )| A、70° | B、68° |
| C、60° | D、72° |




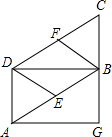 已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点.
已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点.