题目内容
如图，AB∥CD，直线HE⊥MN交MN于E，∠1=130°，则∠2等于________．
40°
分析：由AB∥CD，∠1=130°，根据两直线平行，同位角相等，即可求得∠BEN的度数，由邻补角的性质，即可求得∠AEN的度数，又由HE⊥MN，即可求得∠2的度数．
解答：∵AB∥CD，∠1=130°，
∴∠BEN=∠1=130°，
∴∠AEN=180°-∠BEN=50°，
∵HE⊥MN，
∴∠HEN=90°，
∴∠2=∠HEN-∠AEN=90°-50°=40°．
故答案为：40°．
点评：此题考查了平行线的性质与垂直的定义．此题难度不大，解题的关键是注意掌握两直线平行，同位角相等定理的应用．
分析：由AB∥CD，∠1=130°，根据两直线平行，同位角相等，即可求得∠BEN的度数，由邻补角的性质，即可求得∠AEN的度数，又由HE⊥MN，即可求得∠2的度数．
解答：∵AB∥CD，∠1=130°，
∴∠BEN=∠1=130°，
∴∠AEN=180°-∠BEN=50°，
∵HE⊥MN，
∴∠HEN=90°，
∴∠2=∠HEN-∠AEN=90°-50°=40°．
故答案为：40°．
点评：此题考查了平行线的性质与垂直的定义．此题难度不大，解题的关键是注意掌握两直线平行，同位角相等定理的应用．
练习册系列答案
相关题目
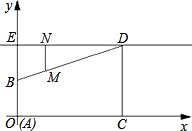横坐标为x，纵坐标为y．
如图，将网格中的三条线段AB、CD、EF沿网格线（水平和铅直方向）平移，使它们首尾相接构成三角形，至少需要移动
