题目内容
反比例函数y=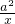
（a≠0）图象经过第________象限；若图象上有两点A（1，y1），B（2，y2），则y1________y2（填“＞”“=”或“＜”）
一，三 ＞
分析：根据反比例函数图象的性质即可得出图象经过第一，三象限，然后把点A，点B代入即可比较大小．
解答：∵a2＞0，
∴反比例函数y=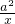（a≠0）图象经过第一，三象限，
把A（1，y1），B（2，y2）代入得：y1=a2，y2=
，
∴y1＞y2，
故答案为：一，三；＞．
点评：本题考查了反比例函数图象上点的坐标特征，难度不大，关键是掌握在y=
（k≠0）中，当k＞0时图象经过第一，三象限，当k＜0时，图象经过第二，四象限．
分析：根据反比例函数图象的性质即可得出图象经过第一，三象限，然后把点A，点B代入即可比较大小．
解答：∵a2＞0，
∴反比例函数y=
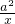（a≠0）图象经过第一，三象限，把A（1，y1），B（2，y2）代入得：y1=a2，y2=
，∴y1＞y2，
故答案为：一，三；＞．
点评：本题考查了反比例函数图象上点的坐标特征，难度不大，关键是掌握在y=
（k≠0）中，当k＞0时图象经过第一，三象限，当k＜0时，图象经过第二，四象限． 
练习册系列答案
每课必练系列答案
相关题目
若点（3，4）是反比例函数y=
的图象上一点，则此函数图象必经过点（ ）
| m2+2m+1 |
| x |
| A、（2，6） |
| B、（-2.6） |
| C、（4，-3） |
| D、（3，-4） |
如图，点A在反比例函数y=
若一次函数y=kx+b的图象如图所示，则抛物线y=x2+kx+b的对称轴位于y轴的