题目内容
若点（3，4）是反比例函数y=
的图象上一点，则此函数图象必经过点（ ）
| m2+2m+1 |
| x |
| A、（2，6） |
| B、（-2.6） |
| C、（4，-3） |
| D、（3，-4） |
分析：根据反比例函数图象上点的坐标特征，k=12，判断各选项中的横纵坐标之积是否等于12．
解答：解：把点（3，4）代入反比例函数y=
，4=
，解得m2+2m+1=k=12，故此函数为y=
，即xy=12，在四个选项中只有A中xy=12．
故选A．
| m2+2m+1 |
| x |
| 2m+1+m2 |
| 3 |
| 12 |
| x |
故选A．
点评：本题考查了反比例函数图象上点的坐标特征，只要点在函数的图象上，则一定满足函数的解析式．反之，只要满足函数解析式就一定在函数的图象上．
练习册系列答案
相关题目
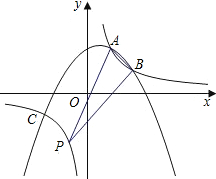如图，抛物线y=ax2+bx+c经过点A（1，2）、B（2，1）和C（-2，-1）三点．
如图，抛物线y=ax2+bx+c经过点A（1，2）、B（2，1）和C（-2，-1）三点．
的图象的一个分支经过点C，并且另个分支与抛物线在第一象限相交．
的图象的一个分支经过点C，并且另个分支与抛物线在第一象限相交．
的图象是否经过点A和点B，试说明理由；
在第三象限的图象上的一个动点，连接AB、PA、PB，请问是否存在这样的一点P使△PAB的面积为3？如果存在，试求出所有符合条件的点P的坐标；如果不存在，请说明理由．
（k≠0）的图象上任一点，过P点分别做x轴，y轴的平行线，若两平行线与坐标轴围成矩形的面积为2，则k的值为 ．