题目内容
8.四边形ABCD中,E、F、G、H分别是四边的中点,对角线AC=BD,则四边形EFGH是( )| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 平行四边形 |
分析 根据三角形中位线的性质,可得EF与GH的关系,根据平行四边的判定,可得EFGH的形状,根据菱形的判定,可得答案.
解答 解:如图: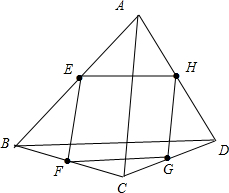 ,
,
∵四边形ABCD中,E、F、G、H分别是四边的中点,
∴EF∥AC,HG∥AC,EF=$\frac{1}{2}$AC,GH$\frac{1}{2}$AC,
∴EF∥HG,EF=GH,
∴EFGH是平行四边形.
同理FG=$\frac{1}{2}$AC.
∵AC=BD,
∴EF=FG,
∴EFGH是菱形,
故选:A.
点评 本题考查了中点四边形,利用了三角形中位线的性质,平行四边形的判定,菱形的判定,注意四边形中点的图形是平行四边形,对角线相等的四边形中点的图形是菱形,对角线互相垂直的四边形中点的图形是矩形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知⊙O1和⊙O2的半径分别是3cm和5cm,圆心距O1O2是4cm,则这两个圆的位置关系是( )
| A. | 外离 | B. | 相交 | C. | 相切 | D. | 内含 |
20.若关于x的一元二次方程2x2-x-n=0没有实数根,则二次函数y=2x2-x-n的图象的顶点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
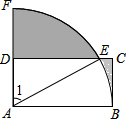 如图,矩形ABCD中,AB=2DA,以A为圆心,AB为半径的弧交DC于E,交AD的延长线于点F.
如图,矩形ABCD中,AB=2DA,以A为圆心,AB为半径的弧交DC于E,交AD的延长线于点F.


