题目内容
如图(1),矩形纸片ABCD,把它沿对角线BD向上折叠,
(1)在图(2)中用实线画出折叠后得到的图形(要求尺规作图,保留作图痕迹,不写作法)
(2)折叠后重合部分是什么图形?说明理由.

考点:
翻折变换(折叠问题)。
分析:
(1)根据折叠的性质,可以作∠BDF=∠BDC,∠EBD=∠CBD,则可求得折叠后的图形.
(2)由折叠的性质,易得∠FDB=∠CDB,又由四边形ABCD是矩形,可得AB∥CD,即可证得∠FDB=∠FBD![]() ,即可证得△FBD是等腰三角形.
,即可证得△FBD是等腰三角形.
解答:
解:(1)做法参考:
方法1:作∠BDG=∠BDC,在射线DG上截取DE=DC,连接BE;
方法2:作∠DBH=∠DBC,在射线BH上截取BE=BC,连接DE;
方法3:作∠BDG=∠BDC,过B点作BH⊥DG,垂足为E
方法4:作∠DBH=∠DBC,过,D点作DG⊥BH,垂足为E;
方法5:分别以D、B为圆心,DC、BC的长为半径画弧,两弧交于点E,连接DE、BE…2分
(做法合理均可得分)
∴△DEB为所求做的图形…3分.
(2)等腰三角形.…4分
证明:∵△BDE是△BDC沿BD折叠而成,
∴△BDE≌△BDC,
∴∠FDB=∠CDB,…5分
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ABD=∠BDC,…6分
∴∠FDB=∠BDC,…7分
∴△BDF是等腰三角形.…8分

点评:
此题考查了矩形的性质、等腰三角形的判定,折叠的性质以及尺规作图.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,一张矩形纸片沿BC折叠,顶点A落在点A′处,第二次过A′,再折叠,使折痕DE∥BC,若AB=2,AC=3,则梯形BDEC的面积为
如图,一张矩形纸片沿BC折叠,顶点A落在点A′处,第二次过A′,再折叠,使折痕DE∥BC,若AB=2,AC=3,则梯形BDEC的面积为
 (2009•郑州模拟)如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(2009•郑州模拟)如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.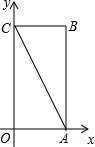 别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M,
别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M, 如图,一张矩形纸片ABCD的长AD=9cm,宽AB=3cm,现将其折叠,使点D与点B重合,则BE=
如图,一张矩形纸片ABCD的长AD=9cm,宽AB=3cm,现将其折叠,使点D与点B重合,则BE=